题目内容
19.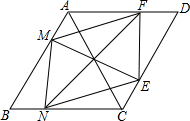 如图,点O是?ABCD对角线AC的中点,过点O的直线ME、NF交边于M、E、N、F,求证:MN$\stackrel{∥}{=}$EF.
如图,点O是?ABCD对角线AC的中点,过点O的直线ME、NF交边于M、E、N、F,求证:MN$\stackrel{∥}{=}$EF.
分析 先证明△AOF≌△CON(ASA),得出AE=CN,同理得出AM=CE,再证明△AMF≌△CEN,得出对应边相等MF=EN,同理得出MN=EF,证出四边形MNEF是平行四边形,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∴∠OAF=∠OCN,
∵O是AC的中点,
∴OA=OC,
在△AOF和△CON中,$\left\{\begin{array}{l}{∠AOF=∠CON}&{\;}\\{OA=OC}&{\;}\\{∠OAF=∠OCN}&{\;}\end{array}\right.$,
∴△AOF≌△CON(ASA),
∴AE=CN,
同理:AM=CE,
在△AMF和△CEN中,$\left\{\begin{array}{l}{AF=CN}&{\;}\\{∠MAF=∠ECN}&{\;}\\{AM=CE}&{\;}\end{array}\right.$
∴△AMF≌△CEN(SAS),
∴MF=EN,
同理:MN=EF,
∴四边形MNEF是平行四边形,
∴MN∥EF,MN=EF.
点评 本题考查了平行四边形的判定与性质以及全等三角形的判定与性质,通过证明三角形全等得出对应边相等证明平行四边形是解决问题的关键.

练习册系列答案
相关题目
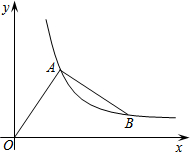 如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则$\frac{b}{a}$的值等于$\frac{1+\sqrt{5}}{2}$.
如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则$\frac{b}{a}$的值等于$\frac{1+\sqrt{5}}{2}$.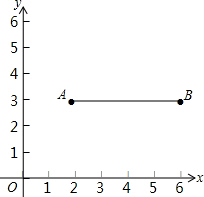 如图,在平面直角坐标系中,已知点A(2,3)、B(6,3)连接AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3)连接AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的“临近点”.