Question

如图，已知⊙O的两条半径OA与OB互相垂直，C为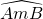上的一点，且AB²+OB²=BC²，求∠OAC的度数．

Answer 1

解：如图，设圆的半径是r，则
AO=r，BO=r，
作直径BD，作BC⊙O的弦BC，使∠DBC=30°，作BC关于直径BD的对称线段BE，
连接EC，BE，ED，AC，
在直角△BED中，可以得∠EBD=30°，
因为线段BE与线段BC关于直线BD对称，
所以BC=BE，
所以BD垂直平分线段CE，
所以=，
所以∠CBD=30°而∠BCA=∠AOB=45°．
在三角形ABC中，
∠OAC=180°-∠ABO-∠CBD-∠ACB-∠BAO=15°．
同理，当E为C时，∠OAC=75°．
故答案为：15°或75°．
分析：先设圆的半径是r，作直径BD，作BC关于直径BD的对称线段BE，连接EC，BE，ED，AC，再由直角三角形的性质即可解答．
点评：本题考查的是圆心角、弧、弦的关系及直角三角形的性质，根据作出辅助线是解答此题的关键．