题目内容
⊙O的半径为6,⊙O的一条弦AB长6 ,以3为半径⊙O的同心圆与直线AB的位置关系是
,以3为半径⊙O的同心圆与直线AB的位置关系是
- A.相离
- B.相交
- C.相切
- D.不能确定
C
分析:作弦AB的弦心距,连接一条半径,根据垂径定理得到半弦是3 .再根据勾股定理得该弦的弦心距=
.再根据勾股定理得该弦的弦心距= =3.则以3为半径⊙O的同心圆与直线AB的位置关系是相切.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
=3.则以3为半径⊙O的同心圆与直线AB的位置关系是相切.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答:作弦AB的弦心距,连接一条半径,
∵⊙O的半径为6,⊙O的一条弦AB长6 ,
,
∴弦的弦心距= =3,
=3,
∴以3为半径⊙O的同心圆与直线AB的位置关系是相切.
故选C.
点评:解决此题的关键是综合运用垂径定理和勾股定理计算弦的弦心距.
分析:作弦AB的弦心距,连接一条半径,根据垂径定理得到半弦是3
 .再根据勾股定理得该弦的弦心距=
.再根据勾股定理得该弦的弦心距= =3.则以3为半径⊙O的同心圆与直线AB的位置关系是相切.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
=3.则以3为半径⊙O的同心圆与直线AB的位置关系是相切.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.解答:作弦AB的弦心距,连接一条半径,
∵⊙O的半径为6,⊙O的一条弦AB长6
 ,
,∴弦的弦心距=
 =3,
=3,∴以3为半径⊙O的同心圆与直线AB的位置关系是相切.
故选C.
点评:解决此题的关键是综合运用垂径定理和勾股定理计算弦的弦心距.

练习册系列答案
相关题目
 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙P内含于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP.若⊙O的半径为3,⊙P的半径为1,则弦AB的长为
如图,⊙P内含于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP.若⊙O的半径为3,⊙P的半径为1,则弦AB的长为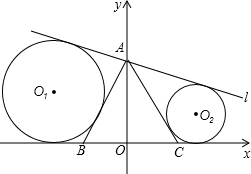
 如图,已知四边形ABCD外接⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,求△ABD的面积.
如图,已知四边形ABCD外接⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,求△ABD的面积.