题目内容
如图，A、B两个小集镇在河流的同侧，分别到河岸L的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米2万元，请你在河岸L上选择水厂的位置M（作图并标注
出来），使铺设水管的费用最节省，并求出总费用是多少？
出来），使铺设水管的费用最节省，并求出总费用是多少？分析：此题的关键是确定点M的位置，需要首先作点A的对称点A′，连接点B和点A′，交l于点M，M即所求作的点．根据轴对称的性质，知：MA+MB=A′B．根据勾股定理即可求解．
解答：
解：作A关于CD的对称点A′，连接A′B与CD，交点为M，点M即为所求作的点．
则可得：DK=A′C=AC=10千米，
∴BK=BD+DK=40千米，
∴AM+BM=A′B=
=50千米，
总费用为50×2=100万元．
解：作A关于CD的对称点A′，连接A′B与CD，交点为M，点M即为所求作的点．则可得：DK=A′C=AC=10千米，
∴BK=BD+DK=40千米，
∴AM+BM=A′B=
| 302+402 |
总费用为50×2=100万元．
点评：本题主要考查轴对称-最短路线问题的知识点，解答本题的关键是找出点M的位置，此题难度不大．
练习册系列答案
相关题目
的图象和反比例函数y=
的图象的两个交点，直线AB与y轴交于点C．
的解集(直接写出答案)．
，-2)，B(1，4)是一次函数
的图象和反比例函数y=
的图象的两个交点，直线AB与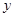
轴交于点C．.
＜0的解集.