题目内容
 在△ABC中,∠BAC的角平分线AN⊥BN,M是BC的中点,已知AB=10,BC=22,则MN=
在△ABC中,∠BAC的角平分线AN⊥BN,M是BC的中点,已知AB=10,BC=22,则MN=分析:延长线段BN,交AC于E,利用已知易证△ABN≌△AEN,所以BN=EN,从而证得MN是△BCE的中位线,所以求出EC,再运用中位线定理求MN.
解答: 解:延长线段BN,交AC于E.
解:延长线段BN,交AC于E.
∵AN平分∠BAC,∴∠BAN=∠EAN.
∵在△ABN与△AEN中,
,
∴△ABN≌△AEN(ASA).
∴AE=AB=10,BN=NE.
又∵M是△ABC的边BC的中点,
故MN=
EC=
(AC-AE)=
(22-10)=6.
故答案是:6.
 解:延长线段BN,交AC于E.
解:延长线段BN,交AC于E.∵AN平分∠BAC,∴∠BAN=∠EAN.
∵在△ABN与△AEN中,
|
∴△ABN≌△AEN(ASA).
∴AE=AB=10,BN=NE.
又∵M是△ABC的边BC的中点,
故MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:6.
点评:本题考查了三角形中位线定理和等腰三角形的判定与性质.
作出辅助线NE即可:
(1)构造出全等三角形(△ABN≌△AEN),从而求出CE的长;
(2)证明MN是中位线,从而轻松解决问题.
作出辅助线NE即可:
(1)构造出全等三角形(△ABN≌△AEN),从而求出CE的长;
(2)证明MN是中位线,从而轻松解决问题.

练习册系列答案
相关题目
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.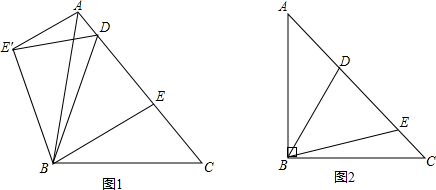
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.