题目内容
 如图△ABC中,BD、CE分别平分∠ABC和∠ACB,∠A=50°,则∠BFC度数为
如图△ABC中,BD、CE分别平分∠ABC和∠ACB,∠A=50°,则∠BFC度数为
- A.130°
- B.115°
- C.120°
- D.100°
B
分析:在△ABC中,根据角平分线的定义及三角形内角和定理,先求得∠ABD+∠ACE的值,从而求得∠CBD+∠ECB的值;然后在△BFC中利用三角形内角和定理求得∠BFC度数.
解答:∵BD、CE分别平分∠ABC和∠ACB,
∴∠ABD=∠CBD,∠ACE=∠ECB;
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠CBD+2∠ECB=180°;
∵∠A=50°,
∴∠CBD+∠ECB=65°;
在△BFC中,
又∵∠BFC+∠CBD+∠ECB=180°,
∴∠BFC=115°.
故选B.
点评:本题主要考查了角平分线的定义及三角形内角和定理.
分析:在△ABC中,根据角平分线的定义及三角形内角和定理,先求得∠ABD+∠ACE的值,从而求得∠CBD+∠ECB的值;然后在△BFC中利用三角形内角和定理求得∠BFC度数.
解答:∵BD、CE分别平分∠ABC和∠ACB,
∴∠ABD=∠CBD,∠ACE=∠ECB;
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠CBD+2∠ECB=180°;
∵∠A=50°,
∴∠CBD+∠ECB=65°;
在△BFC中,
又∵∠BFC+∠CBD+∠ECB=180°,
∴∠BFC=115°.
故选B.
点评:本题主要考查了角平分线的定义及三角形内角和定理.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
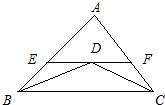

 如图△ABC中,BD=DC,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:AB=AC.
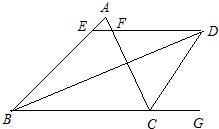
如图△ABC中,BD=DC,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:AB=AC. 已知,如图△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.
已知,如图△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.