题目内容
已知:如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE,求证:OB=OC.

【答案】
见解析
【解析】
试题分析:欲证OB=OC可证明∠1=∠2,由已知发现,∠1,∠2均在直角三角形中,因此证明△BCE与△CBD全等即可.
∵CE⊥AB,BD⊥AC,
∴∠BEC=∠CDB=90°
在Rt△BCE与Rt△CBD中

∴Rt△BCE≌Rt△CBD(HL)
∴∠1=∠2,
∴OB=OC.
考点:本题考查的是直角三角形全等的判定和性质,等腰三角形的判定
点评:解答本题的关键是分析得到欲证OB=OC可证明∠1=∠2。

练习册系列答案
相关题目
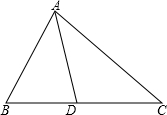 已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD.
已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD. (1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G.
(1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G. 已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE.
已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE. 已知,如图△ABC中,AB=AC,CD⊥AD于D,CD=
已知,如图△ABC中,AB=AC,CD⊥AD于D,CD= 已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为
已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为