题目内容
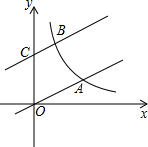 如图,直线y=
如图,直线y=| 1 |
| 2 |
| k |
| x |
| 1 |
| 2 |
| k |
| x |
考点:反比例函数与一次函数的交点问题,一次函数图象与几何变换
专题:
分析:分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,再设A(3x,
x),由于OA=3BC,故可得出B(x,
x+4),再根据反比例函数中k=xy为定值求出k的值即可.
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:分别过点A、B作AD⊥x轴,BE⊥x轴,CF⊥BE于点F,设A(3x,
x),
∵OA=3BC,BC∥OA,CF∥x轴,
∴△BCF∽△AOD,
∴CF=
OD,
∵点B在直线y=
x+4上,
∴B(x,
x+4),
∵点A、B在双曲线y=
上,
∴3x•
x=x•(
x+4),解得x=1,
∴k=3×1×
×1=
.
故答案为
.
| 3 |
| 2 |
∵OA=3BC,BC∥OA,CF∥x轴,

∴△BCF∽△AOD,
∴CF=
| 1 |
| 3 |
∵点B在直线y=
| 1 |
| 2 |
∴B(x,
| 1 |
| 2 |
∵点A、B在双曲线y=
| k |
| x |
∴3x•
| 3 |
| 2 |
| 1 |
| 2 |
∴k=3×1×
| 3 |
| 2 |
| 9 |
| 2 |
故答案为
| 9 |
| 2 |
点评:本题考查的是反比例函数综合题,根据题意作出辅助线,设出A、B两点的坐标,再根据k=xy的特点求出k的值即可.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,数轴上点A,B对应的数分别为1,
如图,数轴上点A,B对应的数分别为1,| 7 |
A、
| ||
B、
| ||
C、1-
| ||
D、2-
|
下列计算正确的是( )
A、
| ||||||||
B、
| ||||||||
C、5
| ||||||||
D、2
|
 某同学为了解所住小区家庭月均用水情况,调查了该小区所有200户家庭,并将调查数据整理如表:
某同学为了解所住小区家庭月均用水情况,调查了该小区所有200户家庭,并将调查数据整理如表: 如图,延长线段AB到C,使BD=3AB,点D是线段BC的中点,CD=6,求线段AC的长.
如图,延长线段AB到C,使BD=3AB,点D是线段BC的中点,CD=6,求线段AC的长.