题目内容
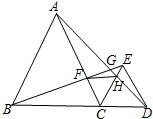
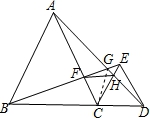
如图,已知△ABC与△CDE都是等边三角形,点B、C、D在同一条直线上,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AGB=60°;③BF=AH;④△CFH是等边三角形;⑤连CG,则∠BGC=∠DGC.其中正确的个数是( )
A.2 B.3 C.4 D.5
D
【考点】全等三角形的判定与性质;等边三角形的判定与性质.
【分析】利用等边三角形的性质得出条件,可证明:△BCE≌△ACD;利用△BCE≌△ACD得出∠CBF=∠CAH,再运用平角定义得出∠BCF=∠ACH,进而得出△BCF≌△ACH因此BF=AH.由CF=CH和∠ACH=60°根据“有一个角是60°的三角形是等边三角形可得△CFH是等边三角形.连接CG,根据∠AGB=∠ACB=60°,∠C BG=∠CAG,推出点A,B,C,G四点共圆,根据圆周角定理得到∠BGC=∠BAC=60°,由圆内接四边形的性质得到∠CGD=∠ABC=60°,于是得到∠BGC=∠DGC.
BG=∠CAG,推出点A,B,C,G四点共圆,根据圆周角定理得到∠BGC=∠BAC=60°,由圆内接四边形的性质得到∠CGD=∠ABC=60°,于是得到∠BGC=∠DGC.
【解答】解:∵∠BCA=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
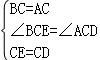 ,
,
∴△BCE≌△ACD(SAS);故①正确;
∵△BCE≌△ACD,
∴∠CBF=∠CAH.
∵∠BFC=∠AFG,
∴∠AGB=∠ACB=60°,故②正确;
在△BCF 和△ACH中,
和△ACH中,
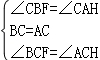 ,
,
∴△BCF≌△ACH(ASA),
∴CF=CH,BF=AH;故③正确;
∵CF=CH,∠ACH=60°,
∴△CFH是等边三角形;故④正确;
连接CG,
∵∠AGB=∠ACB=60°,∠CBG=∠CAG,
∴点A,B,C,G四点共圆,
∴∠BGC=∠BAC=60°,
∵∠CGD=∠ABC=60°,
∴∠BGC=∠DGC,故⑤正确.
故选D.
【点评】本题考查了三角形全等的判定和性质及等边三角形的性质;普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS.同时还要结合等边三角形的性质,创造条件证明三角形全等是正确解答本题的关键.

 下一个最大的正方形,那么剩余图形的周长是__________.
下一个最大的正方形,那么剩余图形的周长是__________. ;
; ﹣
﹣ +
+ ;
;  是关于x的四次三项式,则m的值是( )
是关于x的四次三项式,则m的值是( ) <0,则x+y的值是__________.
<0,则x+y的值是__________.