题目内容
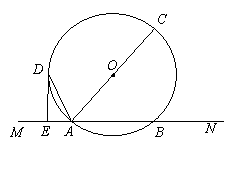
已知如图,直线MN交⊙O于A、B两点,AC是直径,AD平分![]() CAM交⊙O于D,过D作DE
CAM交⊙O于D,过D作DE![]() MN于E.
MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
 |
(1)证明:连结OD.
∵AD平分![]() CAM ∴
CAM ∴![]() DAC=
DAC=![]() DAE
DAE
∵AO=DO ∴![]() DAC=
DAC=![]() ADO
ADO
∴![]() ADO =
ADO =![]() DAE
DAE
∵DE⊥MN ∴![]() DAE+
DAE+![]() ADE=90°
ADE=90°
∴![]() ADO+
ADO+![]() ADE=90° 即
ADE=90° 即![]() ODE=90°
ODE=90°
∴OD⊥DE ∴DE是⊙O的切线
(2)作AF⊥OD于F,则四边形AEDF是矩形.
∴DF=AE=3cm,AF=DE=6cm
设⊙O半径为r
∵Rt△AOF中,![]()
∴![]()
解得r=7.5

练习册系列答案
相关题目
 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
 已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.∠ADE=30°,⊙O的半径为2,图中阴影部分的面积为
已知:如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN,垂足为E.∠ADE=30°,⊙O的半径为2,图中阴影部分的面积为 已知,如图,直线MN交⊙O于A、B两点,AC是直径,DE切⊙O于D,DE⊥MN于E.
已知,如图,直线MN交⊙O于A、B两点,AC是直径,DE切⊙O于D,DE⊥MN于E.