题目内容
已知：如图，直线MN交⊙O于A、B两点，AC是直径，AD平分∠CAM交⊙O于点D，过点D作DE⊥MN，垂足为E．∠ADE=30°，⊙O的半径为2，图中阴影部分的面积为| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
| 3 |
分析：连接OB，易证△OAB是等边三角形，求得扇形OAB的面积减去△OAB的面积，即可求得阴影部分的面积．
解答：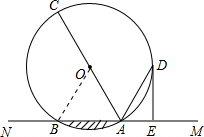
解：连接OB．
∵DE⊥MN，
∴直角△AED中，∠DAE=90°-∠ADE=60°，
∵AD平分∠CAM交⊙O于点D，
∴∠CAM=2∠DAE=120°，
∴∠OAB=60°，
∵OA=OB，
∴△AOB是等边三角形．
∴S△AOB=
=
，
S扇形OAB=
=
，
则阴影部分的面积为
-
．
故答案是：
-
．
解：连接OB．∵DE⊥MN，
∴直角△AED中，∠DAE=90°-∠ADE=60°，
∵AD平分∠CAM交⊙O于点D，
∴∠CAM=2∠DAE=120°，
∴∠OAB=60°，
∵OA=OB，
∴△AOB是等边三角形．
∴S△AOB=
| ||
| 4 |
| 3 |
S扇形OAB=
| 60π×22 |
| 360 |
| 2π |
| 3 |
则阴影部分的面积为
| 2π |
| 3 |
| 3 |
故答案是：
| 2π |
| 3 |
| 3 |
点评：本题考查了扇形的面积的计算，正确证明△OAB是等边三角形是关键．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．
（2013•路北区三模）已知：如图，直线MN交⊙O于A、B两点，AC是直径，AD平分∠CAM交⊙O于点D，过点D作DE⊥MN，垂足为E．
交于点G，垂足分别是E、F，AC是⊙O的弦，
已知，如图，直线MN交⊙O于A、B两点，AC是直径，DE切⊙O于D，DE⊥MN于E．