题目内容
16.已知a、b为有理数,x、y分别表示$5-\sqrt{7}$的整数部分和小数部分,且满足axy+by2=1,求a+b的值.分析 运用估算的方法,先确定x,y的值,再代入xy+by2=1中求出a、b的值.
解答 解:∵2<5-$\sqrt{7}$<3,
∴x=2,y=3-$\sqrt{7}$;
∵axy+by2=1,
∴a•2•(3-$\sqrt{7}$)+b(3-$\sqrt{7}$)2=1,即(-2a-6b)$\sqrt{7}$+(6a+16b-1)=0.
∵a、b为有理数,
∴$\left\{\begin{array}{l}{-2a-6b=0}\\{6a+16b-1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$,
∴a+b=1.
点评 本题考查了无理数的大小的估算.解题关键是确定无理数的整数部分即可解决问题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
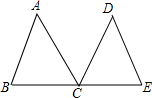 如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC.
如图,已知:点C是线段BE的中点,AC平分∠DCB,CD平分∠ACE,AC=DC.