题目内容
如图，已知1号、4号两个正方形的面积和为8，2号、3号两个正方形的面积和为5，则a、b、c三个正方形的面积和为 ．
考点：全等三角形的判定与性质,勾股定理,正方形的性质
专题：
分析：由直角三角形的勾股定理以及正方形的面积公式，不难发现：a的面积等于1的面积加上2的面积，b的面积等于2加上3，据此可以求出三个的面积的和．
解答：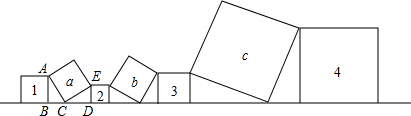
解：如下图所示：
∵1，2，a三个四边形均为正方形，
∴∠ACB+∠BAC=90°，∠ACB+∠DCE=90°，
∴∠BAC=∠DCE，
在△ABC和△CDE中
∴△ABC≌△CDE（AAS），
∴BC=DE，
∴AC2=AB2+BC2，
∴a的面积等于1的面积加上2的面积，
即Sa=S1+S2，
同理可得出，Sb=S2+S3，Sc=S3+S4，
∴Sa+Sb+Sc=Sa=S1+S2+S2+S3+S3+S4=8+5+5=18．
故答案为：18．
解：如下图所示：∵1，2，a三个四边形均为正方形，
∴∠ACB+∠BAC=90°，∠ACB+∠DCE=90°，
∴∠BAC=∠DCE，
在△ABC和△CDE中
|
∴△ABC≌△CDE（AAS），
∴BC=DE，
∴AC2=AB2+BC2，
∴a的面积等于1的面积加上2的面积，
即Sa=S1+S2，
同理可得出，Sb=S2+S3，Sc=S3+S4，
∴Sa+Sb+Sc=Sa=S1+S2+S2+S3+S3+S4=8+5+5=18．
故答案为：18．
点评：本题考查了勾股定理的运用，结合正方形的面积公式求解是解题关键．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在直角坐标系内，设A（0，0），B（4，0），C（t+4，4），D（t，4）（t为实数），记N为平行四边形ABCD内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则N的值可能为
如图，若将宽为
如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，当四边形ABCD的边满足下列（ ）条件时，四边形EFGH是菱形．| A、AB∥DC |
| B、AC=BD |
| C、AC⊥BD |
| D、AB=DC |