题目内容
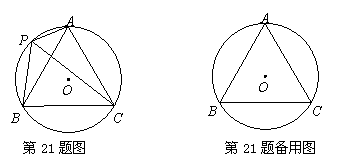
如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断 ABC的形状:______________;
ABC的形状:______________;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
 |
解:(1)等边三角形.
(2)PA+PB=PC.
证明:如图1,在PC上截取PD=PA,连接AD.
∵∠APC=60°,
∴△PAD是等边三角形.
 ∴PA=AD,∠PAD=60°.
∴PA=AD,∠PAD=60°.
又∵∠BAC=60°,
∴∠PAB=∠DAC.
∵AB=AC,
∴△PAB≌△DAC.
∴PB=DC.
∵PD+DC=PC,
∴PA+PB=PC.
 (3)当点P为
(3)当点P为 的中点时,四边形APBC面积最大.
的中点时,四边形APBC面积最大.
理由如下:如图2,过点P作PE⊥AB,垂足为E,
过点C作CF⊥AB,垂足为F,
∵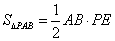 ,
,  .
.
∴S四边形APBC=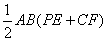 .
.
∵当点P为弧AB的中点时,PE+CF =PC, PC为⊙O直径,
∴四边形APBC面积最大.
又∵⊙O的半径为1,
 ∴其内接正三角形的边长AB=
∴其内接正三角形的边长AB= .
.
∴S四边形APBC= =
= .
.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目

 如图,要制作一个圆锥形
如图,要制作一个圆锥形 0.77,cos50º
0.77,cos50º
 中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) ,AC=13,cos∠B=
,AC=13,cos∠B= ,则BC边长为( )
,则BC边长为( )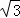 ,∠AFM=15°,则AM= 3﹣
,∠AFM=15°,则AM= 3﹣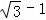 .
.