题目内容
B
【解析】连接EC,交AD于点P,次数EP+BP的值最小,过点E作EF⊥BC,则有BD=CD=2,由勾股定理,可
得AD=2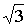 ,同时可得EF∥AD,△BEF∽△BAD,所以
,同时可得EF∥AD,△BEF∽△BAD,所以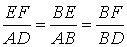 ,解得BF=1.5,FD=0.5,EF=
,解得BF=1.5,FD=0.5,EF= ,所以EC=
,所以EC=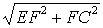 =
= ,所求的最小值是
,所求的最小值是 .
.
(1)AE∥BD,且AE=BD.(2)16;(3)当∠ACB=60°时,四边形ABFE为矩形.
【解析】(1)AE∥BD,且AE=BD.理由如下:∵将△ABC绕点C顺时针旋转180°得到△DEC,∴△ABC≌△DEC,∴AB=DE,∠ABC=∠DEC,∴AB∥DE,∴四边形ABDE是平行四边形,∴AE∥BD,且AE=BD;
(2)由(1)得四边形ABFE为平行四边形,∴AC=CF,BC=CE,∴根据等底同高得到S△ABC=S△ACE=S△BCF=S△CEF=4,S四边形ABFE=4S△ABC=16cm2;
(3)当∠ACB=60°时,四边形ABFE为矩形.
理由是:AB=AC,∠ACB=60°,∴△ABC是等边三角形,∴BC=AC,∠BAC=60°,∴∠ACE=120°.又BC=CE,AC=CF,∴∠EAC=∠CEA=30°,∴∠BAE=90°,同理可证其余三个角也为直角.∴四边形ABFE为矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
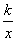 ,则k=
,则k= 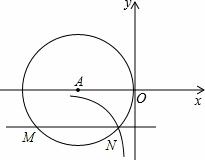

 如图:想得到题意中的俯视图,只需在图(2)中的A位置添加一个或叠放1个或两个小正方形,故组成这个几何体的小正方形的个数为4个或5个.
如图:想得到题意中的俯视图,只需在图(2)中的A位置添加一个或叠放1个或两个小正方形,故组成这个几何体的小正方形的个数为4个或5个.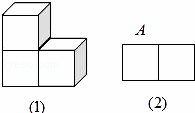
 ,则一次函数
,则一次函数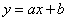 与反比例函数
与反比例函数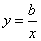 在同一直角坐标系中的图象大致可能是( )
在同一直角坐标系中的图象大致可能是( ) B.
B. C.
C. D.
D.
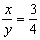 ,则
,则
 分别与AB,CD相交,若∠1=120°,则∠2等于( )
分别与AB,CD相交,若∠1=120°,则∠2等于( )