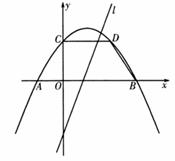
题目内容
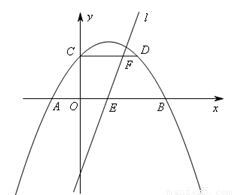
如图,抛物线 关于直线
关于直线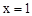 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D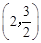 在抛物线上,直线
在抛物线上,直线 是一次函数
是一次函数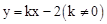 的图象,点O是坐标原点.
的图象,点O是坐标原点.
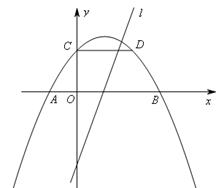
(1)求抛物线的解析式;
(2)若直线 平分四边形OBDC的面积,求k的值.
平分四边形OBDC的面积,求k的值.
(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线 交于M、N两点,问在y轴正半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴对称?若存在,求出P点坐标;若不存在,请说明理由.
交于M、N两点,问在y轴正半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴对称?若存在,求出P点坐标;若不存在,请说明理由.
(1)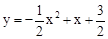 (2)
(2) (3)存在一点P(0,2),使直线PM与PN总是关于y轴对称
(3)存在一点P(0,2),使直线PM与PN总是关于y轴对称
【解析】解:(1)∵抛物线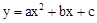 关于直线x=1对称,AB=4,∴A(-1,0),B(3,0) 。
关于直线x=1对称,AB=4,∴A(-1,0),B(3,0) 。
∴可设抛物线的解析式为 。
。
∵点D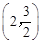 在抛物线上,∴
在抛物线上,∴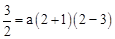 ,解得
,解得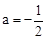 。
。
∴抛物线的解析式为 ,即
,即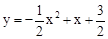 。
。
(2)由(1)知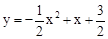 ,令x=0,得C(0,
,令x=0,得C(0, 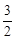 ),
),
∴CD//AB。
令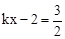 ,得l与CD的交点F(
,得l与CD的交点F(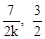 ),
),
令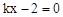 ,得l与x轴的交点E(
,得l与x轴的交点E(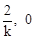 ),
),
由S四边形OEFC=S四边形EBDF得:OE+CF=DF+BE,
即: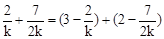 ,解得
,解得 。
。
∴当 时,直线
时,直线 平分四边形OBDC的面积。
平分四边形OBDC的面积。
(3)∵ ,
,
∴把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为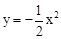 。
。
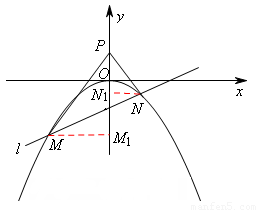
假设在y轴上存在一点P(0,t),t>0,使直线PM与PN关于y轴对称,过点M、N分别向y轴作垂线MM1、NN1,垂足分别为M1、N1,
∵∠MPO=∠NPO,∴Rt△MPM1∽Rt△NPN1。
∴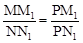 ①。
①。
不妨设M(xM,yM)在点N(xN,yN)的左侧,
因为P点在y轴正半轴上,则①式变为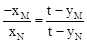 。
。
又∵ ,
,
∴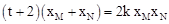 ②。
②。
把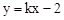 代入
代入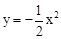 中,整理得
中,整理得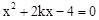 。
。
∴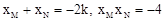 ,代入②得
,代入②得 ,解得t=2,符合条件。
,解得t=2,符合条件。
∴在y轴上存在一点P(0,2),使直线PM与PN总是关于y轴对称。
(1)由已知求出点A,B的坐标,设出交点式,将点D 的坐标代入即可求得抛物线的解析式。
(2)如图,将S四边形OEFC和S四边形EBDF用k表示,根据S四边形OEFC=S四边形EBDF列方程求解即可。
(3)求出平移后的抛物线解析式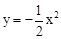 ,假设在y轴上存在一点P(0,t),t>0,使直线PM与PN关于y轴对称,过点M、N分别向y轴作垂线MM1、NN1,垂足分别为M1、N1,不妨设M(xM,yM)在点N(xN,yN)的左侧,由Rt△MPM1∽Rt△NPN1得
,假设在y轴上存在一点P(0,t),t>0,使直线PM与PN关于y轴对称,过点M、N分别向y轴作垂线MM1、NN1,垂足分别为M1、N1,不妨设M(xM,yM)在点N(xN,yN)的左侧,由Rt△MPM1∽Rt△NPN1得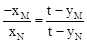 ,即
,即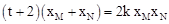 。把
。把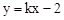 代入
代入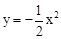 中,整理得
中,整理得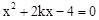 ,根据一元二次方程根与系数的关系得
,根据一元二次方程根与系数的关系得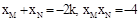 代入
代入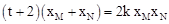 ,即可求得t=2。
,即可求得t=2。

 一本好题口算题卡系列答案
一本好题口算题卡系列答案 关于直线
关于直线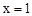 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D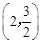 在抛物线上,直线
在抛物线上,直线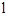 是一次函数
是一次函数 的图象,点O是坐标原点.
的图象,点O是坐标原点.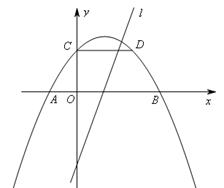
 与直线AB交于点A(-1,0),B(4,
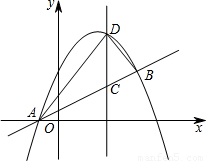
与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.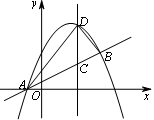
 如图,抛物线
如图,抛物线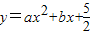 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.