题目内容
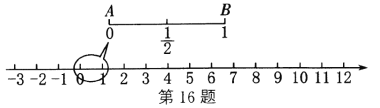
【题目】陈老师从拉面的制作中受到启发，设计了一个数学问题:如图，在数轴上截取从原点到1的对应点的线段
，对折后(点
与
重合)再均匀地拉成1个单位长度的线段，这一过程称为一次操作(如在第一次操作后，原线段上的
和
均变成
，变成1等).那么在线段上(除、)的点中，在第
次操作后，恰好被拉到与1重合的点所对应的数为________________.
【答案】
【解析】
根据题意，可知下一次的操作把上一次的对应点正好扩大了2倍．因为第一次操作后，
原线段AB上的
，
均变成
，则第二次操作后，恰好被拉到与1重合的点所对应的数是 和 ，则它们的和可求．根据题意，将恰好被拉到与1重合的点所对应的坐标列出数据，找出规律，列出通式即可．
根据题意，得
操作次数 变化点 重合点 | 1 | 2 | 3 | 4 |
1 |
|
|
|
|
1 |
|
|
|
第一次操作后，原线段AB上的变为1，
第二次操作后，恰好被拉到与1重合的点所对应的数有21=2个，分别是
和，其和为1，
第三次操作后，恰好被拉到与1重合的点所对应的数有22=4个，分别是
、
、
和
，其和为2，
…，
可以推出第n次操作后，恰好被拉到与1重合的点所对应的数的通式为
、
…
，
故答案为：
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
