��Ŀ����
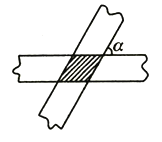
����Ŀ����֪����ͼ��1��������AM������BN��AB�����ǵĹ����ߣ���D��C�ֱ���AM��BN���˶�����D���A���غϡ���C���B���غϣ���E��AB���ϵĶ��㣨��E��A��B���غϣ������˶�������ʼ�ձ���DE��EC��
��1����֤����ADE�ס�BEC��
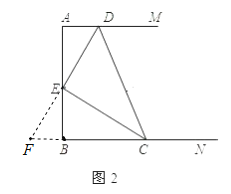
��2����ͼ��2��������EΪAB�ߵ��е�ʱ����֤��AD+BC=CD��
��3���� AD+DE=AB=![]() ʱ����AE=m����̽������BEC���ܳ��Ƿ���mֵ�йأ����йأ����ú���m�Ĵ���ʽ��ʾ��BEC���ܳ������أ���˵�����ɣ�
ʱ����AE=m����̽������BEC���ܳ��Ƿ���mֵ�йأ����йأ����ú���m�Ĵ���ʽ��ʾ��BEC���ܳ������أ���˵�����ɣ�

���𰸡���1�������������2�������������3��![]() ���ܳ���mֵ�أ��������������
���ܳ���mֵ�أ��������������
��������
��1����ֱ������ABCD�С�AΪֱ�ǣ��õ�������ADEΪֱ�������Σ��ɵó�����ǻ��࣬����DE��EC��ֱ�����ô�ֱ�Ķ���õ���DECΪֱ�ǣ�����ƽ�ǵĶ����Ƴ�һ�Խǻ��࣬����ͬ�ǵ������ȿɵó�һ�Խ���ȣ�����һ��ֱ����ȣ��������Զ�Ӧ����ȵ������������ƿɵ�֤��
��2���ӳ�DE��CB����F��֤����ADE�ա�BFE������ȫ�������ε����ʵõ�DE=FE��AD=BF��CE��DE���õ�ֱ��CE���߶�DF�Ĵ�ֱƽ���ߣ����߶δ�ֱƽ���ߵ����ʵ�DC=FC�����ɵõ����ۣ�
��3����BEC���ܳ���m��ֵ�أ�����Ϊ����AD=x����AD+DE=a����ʾ��DE����ֱ��������ADE�У����ù��ɶ����г���ϵʽ������������٣���AB��AE=EB����ʾ��BE�����ݣ�1���õ�����ADE�ס�BEC�������Ƶñ����������Ա�ʾ����ʽ�Ӵ��룬��ʾ��BC��EC����EB+EC+BC��ʾ��������EBC���ܳ�����ȡa��m��ͨ�ֲ�����ͬ��ĸ��ʽ�ļӷ�������㣬������ƽ���ʽ��������ڣ����ٴ���ڣ�Լ�ֺ�õ�һ������m��ʽ�ӣ����ܳ���m�أ�
��1����ֱ������ABCD�У���A=90�㣬
���ADE+��AED=90�㣬
�֡�DE��CE��
���DEC=90�㣬
���AED+��BEC=90�㣬
���ADE=��BEC��
�֡ߡ�A=��B=90�㣬
���ADE�ס�BEC��
��2���ӳ�DE��CB����F����ͼ2��ʾ��
��AD��BC��
���A=��EBF����ADE=��F��
��E��AB���е㣬
��AE=BE��
�ڡ�ADE�͡�BFE�У��ߡ�A=��EBF����ADE=��F��AE=BE��
���ADE�ա�BFE��
��DE=FE��AD=BF��
��CE��DE��
��ֱ��CE���߶�DF�Ĵ�ֱƽ���ߣ�
��DC=FC��
��FC=BC+BF=BC+AD��
��AD+BC=CD��
��3����BEC���ܳ���m��ֵ�أ�����Ϊ��
��AD=x����AD+DE=AB=a���ã�DE=a��x��
��Rt��AED�У����ݹ��ɶ����ã�AD2+AE2=DE2����x2+m2=(a��x)2��
�����ã�a2��m2=2ax������
�ڡ�EBC�У���AE=m��AB=a���ã�BE=AB��AE=a��m��
���ɣ�1��֪��ADE�ס�BEC��
��![]() ����
����![]() ��
��
��ã�BC![]() ��EC
��EC![]() ��
��
���BEC���ܳ�=BE+BC+EC=(a��m)![]()
=(a��m)(1![]() )=(a��m)
)=(a��m)![]()
![]() ������
������
�Ѣٴ���ڵã���BEC���ܳ�=BE+BC+EC![]() 2a��
2a��
���BEC���ܳ���m�أ�

 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�