题目内容
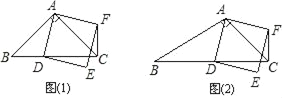
【题目】已知：如图，在矩形
中，
是对角线，点
为矩形外一点且满足
，
，
交
于点
，连接
，过点作
交于
．
（1）若
，
，求矩形的面积；
（2）若
，试判断线段、
、
之间的关系，并证明．
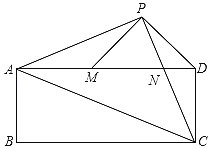
【答案】（1）15；（2）
，证明见解析.
【解析】
（1）由等腰直角三角形的性质可得
，由勾股定理求出
，
，，即可求矩形ABCD的面积；
（2）由矩形的性质可得∠ADC＝∠APC＝90°，可证点A，点C，点D，点P四点共圆，可得∠PDA＝∠PCA＝45°，∠PCD＝∠PAD，∠DPC＝∠DAC，然后证明△ADE≌△ADC，△PAN≌△PEC，可得AC＝AE，PN＝PE，即可得出结论．
解：（1）
，
，
，
，
，
∴
，
，，
；
（2）；
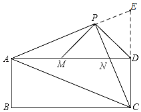
证明：如图，延长
，
交于点
，
，，
，
，
四边形
是矩形
，
点
，点
，点
，点
四点共圆，
，
，
，
，
，
，
∵
，
，
，
，
∵
，
，
，
，
，
，
，
，
，
.
练习册系列答案
相关题目
