题目内容
17.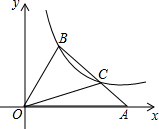 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{3}{x}$(x>0)的图象上,则△OAB的面积等于$\frac{9}{2}$.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{3}{x}$(x>0)的图象上,则△OAB的面积等于$\frac{9}{2}$.
分析 作BD⊥x轴于D,CE⊥x轴于E,则BD∥CE,得出$\frac{CE}{BD}$=$\frac{AE}{AD}$=$\frac{AC}{AB}$=$\frac{1}{2}$,设CE=x,则BD=2x,根据反比例函数的解析式表示出OD=$\frac{3}{2x}$,OE=$\frac{3}{x}$,OA=$\frac{9}{2x}$,然后根据三角形面积求得即可.
解答  解:作BD⊥x轴于D,CE⊥x轴于E,
解:作BD⊥x轴于D,CE⊥x轴于E,
∴BD∥CE,
∴$\frac{CE}{BD}$=$\frac{AE}{AD}$=$\frac{AC}{AB}$,
∵OC是△OAB的中线,
∴$\frac{CE}{BD}$=$\frac{AE}{AD}$=$\frac{AC}{AB}$=$\frac{1}{2}$,
设CE=x,则BD=2x,
∴C的横坐标为$\frac{3}{x}$,B的横坐标为$\frac{3}{2x}$,
∴OD=$\frac{3}{2x}$,OE=$\frac{3}{x}$,
∴DE=$\frac{3}{x}$-$\frac{3}{2x}$=$\frac{3}{2x}$,
∴AE=DE=$\frac{3}{2x}$,
∴OA=$\frac{3}{x}$+$\frac{3}{2x}$=$\frac{9}{2x}$,
∴S△OAB=$\frac{1}{2}$OA•BD=$\frac{1}{2}$×$\frac{9}{2x}$×2x=$\frac{9}{2}$.
故答案为$\frac{9}{2}$.
点评 本题考查了反比例函数系数k的几何意义,平行线分线段成比例定理,求得BD,OA长是解题关键.

练习册系列答案
相关题目
2.已知一次函数y=x+b与反比例函数y=$\frac{4}{x}$的图象相交于点A(1,m).
(1)求一次函数的解析式;
(2)这个一次函数图象沿y轴向下平移4个单位,求平移后的图象与x轴的交点坐标.
(1)求一次函数的解析式;
(2)这个一次函数图象沿y轴向下平移4个单位,求平移后的图象与x轴的交点坐标.
7.下列事件是随机事件的是( )
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 购买一张福利彩票,中奖 | |
| C. | -2的绝对值小于0 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
 如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为2.9米(结果精确到0.1米,参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为2.9米(结果精确到0.1米,参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73).
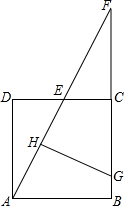 如图,ABCD是边长为a的正方形,E是CD中点,AE和BC的延长线相交于点F,AE的垂直平分线交AE、BC于H、G,求线段FG的长.
如图,ABCD是边长为a的正方形,E是CD中点,AE和BC的延长线相交于点F,AE的垂直平分线交AE、BC于H、G,求线段FG的长.