Question

（2011•鞍山一模）如图，在平面直角坐标系中，直线y=-

3

3

x+

3

交x轴于A点，交y轴于B点，点C是线段AB的中点，连接OC，然后将直线OC绕点C逆时针旋转30°交x轴于点D，则△ODC的面积为

3

4

．

Answer 1

分析：通过直线的解析式可以求出A、B的坐标，从而求出OA、OB的长度，再利用勾股定理求出AB的长度，利用三角函数值还可以求出∠BAO=30°，通过直角三角形的性质可以求得△BOC为等边三角形，在△ADC中作出AD边上的高，用解直角三角形的方法求出其高及AD的长度就可以求出OD的长度，从而求出面积．

解答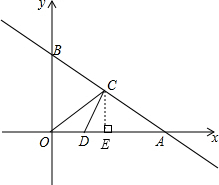：解：作CE⊥AD于点E，
∴∠AEC=90°．
∵y=-

3

3

x+

3

，
∴x=0时，y=

3

，即OB=

3

y=0时，x=3，即OA=3，
在Rt△ABO中，由勾股定理得：
AB=2

3

，
∴sin∠OAB=

OB

AB

=

1

2

，
∴∠OAB=30°，∠OBA=60°，OB=

1

2

AB
∵点C是线段AB的中点，
∴OC=BC=AC=

1

2

AB=

3

∴OC=OB=BC=

3

，∠COA=∠CAO=30°
∴△BOC为等边三角形，∠OCA=120°
∵∠OCD=30°，
∴∠ACD=90°
∴在Rt△ACD中由勾股定理得：
CD=1，AD=2，
∴OD=1，
在Rt△ACE中由勾股定理得：
CE=

3

2

∴S_△OCD=

1× 3 2

2

=

3

4

．

故答案为：

3

4

．

点评：本题是一道一次函数的综合试题，考查了一次函数的图象，直角三角形斜边上中线的运用，旋转的性质，勾股定理的运用，三角形的面积公式．