题目内容
不透明的口袋中装有除颜色外其余均相同的2个白球、2个黄球、4个绿球，从中任取一球出来，它不是黄球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：概率公式
专题：
分析：由不透明的口袋中装有除颜色外其余均相同的2个白球、2个黄球、4个绿球，直接利用概率公式求解即可求得答案．
解答：解：∵不透明的口袋中装有除颜色外其余均相同的2个白球、2个黄球、4个绿球，
∴从中任取一球出来，它不是黄球的概率是：
=
．
故选B．
∴从中任取一球出来，它不是黄球的概率是：
| 2+4 |
| 2+2+4 |
| 3 |
| 4 |
故选B．
点评：此题考查了概率公式的应用．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
关于x的方程ax2+bx+c=0，若满足a-b+c=0，则方程（ ）
| A、没有实数根 |
| B、必有两相等实数根 |
| C、必有一根为1 |
| D、必有一根为-1 |
组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（ ）
| A、x（x+1）=28 | ||
B、
| ||
| C、x（x+1）=28 | ||
| D、x（x-1）=28 |
已知x=-1是方程2x+m=4的解，则m的值是（ ）
A、
| ||
B、
| ||
| C、6 | ||
| D、2 |
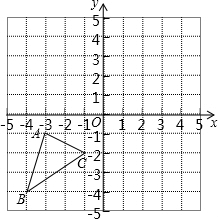如图，在正方形网格中，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：