题目内容
如图,在平面直角坐标系中,⊙O的半径为2,AC、BD是⊙O的两条相互垂直的弦,垂足为M(1, ),则四边形ABCD的面积的最大值与最小值的差为___ ___.
),则四边形ABCD的面积的最大值与最小值的差为___ ___.

 ),则四边形ABCD的面积的最大值与最小值的差为___ ___.
),则四边形ABCD的面积的最大值与最小值的差为___ ___. 
2 ﹣4.
﹣4.
 ﹣4.
﹣4.试题分析:当AC∥x轴时,BD∥y轴,时 此时四边形ABCD的面积最大,
连接OB、OC,设AC,BD分别交x,y轴于点F,E,

∵M(1,
 ),
),∴OE=
 ,OF=1,
,OF=1,∴由勾股定理得BE=
 ,CF=
,CF=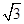 ,
,∵ME=1,
∴BM=
 +1,DM=
+1,DM= ﹣1,AM=
﹣1,AM=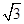 ﹣
﹣ ,CM=
,CM=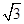 +
+ ,
,∴S四边形ABCD=S△BCM+S△ABM+S△ADM+S△CDM,
=

=
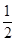 ×4
×4 ,
,=2
 ;
;当弦BD经过圆心时,此时四边形ABCD的面积最小,BD=4,
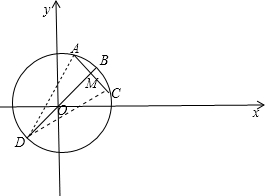
∵M(1,
 )
)∴OM=
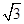 ,MC=1,根据垂径定理,AC=2MC=2,
,MC=1,根据垂径定理,AC=2MC=2,∴S四边形ABCD=S△BAC+S△DAC=
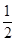 AC•BM+
AC•BM+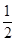 AC•DM=
AC•DM=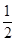 AC•BD=4.
AC•BD=4.∴四边形ABCD面积最大值与最小值的差(2
 ﹣4).
﹣4).故答案是2
 ﹣4.
﹣4.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,求OD的长.
,求OD的长.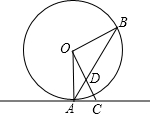
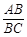 =k.
=k.