题目内容
7.如图,正方形网络中的每个小正方形边长都为1,每个小正方形的顶点叫格点,在图中画出符合下列条件的一个图形.(1)在左图中画一个直角△ABC,使它的顶点都在格点上,且斜边长AB为$\sqrt{10}$;
(2)在右图中画一个菱形ABCD,使它的顶点都在格点上,且边长AB为$\sqrt{5}$.

分析 (1)画直角△ABC,使得两直角边为1与3,斜边即为所求;
(2)画菱形ABCD,使得边长AB为$\sqrt{5}$.
解答 解:(1)如图所示:
△ABC中,AC=3,BC=1,∠ACB=90°,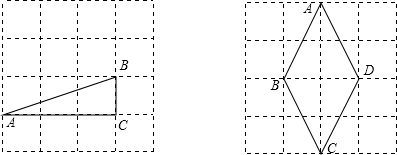 由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$,
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$,
直角△ABC即为所求;
(2)如图所示:
∵AC⊥BD,
∴AB=BC=CD=DA=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴四边形ABCD是菱形,
∴菱形ABCD即为所求.
点评 本题考查了作图-复杂作图、勾股定理、勾股定理的逆定理以及菱形的判定;熟练掌握勾股定理,并能进行推理计算与作图是解决问题的关键.

练习册系列答案
相关题目
16. 如图,线段AB=10,M是AB中点,点N在AB上,且BN=2,则线段MN的长为( )
如图,线段AB=10,M是AB中点,点N在AB上,且BN=2,则线段MN的长为( )
 如图,线段AB=10,M是AB中点,点N在AB上,且BN=2,则线段MN的长为( )
如图,线段AB=10,M是AB中点,点N在AB上,且BN=2,则线段MN的长为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
18.星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的$\frac{5}{6}$,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
| 进价(元/台) | 售价(元/台) | |
| 电饭煲 | 200 | 250 |
| 电压锅 | 160 | 200 |
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的$\frac{5}{6}$,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
15.能把一个三角形分成面积相等的两部分的是该三角形的( )
| A. | 角平分线 | B. | 中线 | ||
| C. | 高 | D. | 一边的垂直平分线 |
19.下列大学的校徽图案是轴对称图形的是( )
| A. |  清华大学 | B. |  北京大学 | C. |  北京人民大学 | D. |  浙江大学 |
 如图,已知线段a、b,请你用直尺和圆规画一条线段,使它等于2a-b.
如图,已知线段a、b,请你用直尺和圆规画一条线段,使它等于2a-b. 单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制出如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵及以上的人数占总人数的( )
单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制出如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵及以上的人数占总人数的( )