题目内容
已知a-b=-3,b-c=-4,则(a-b)2+(b-c)2+(a-c)2= .
考点:代数式求值
专题:
分析:先求出a-c的值,再整体代入,即可得出答案.
解答:解:∵a-b=-3,b-c=-4,
∴两式相加得:a-c=-7,
∴(a-b)2+(b-c)2+(a-c)2
=(-3)2+(-4)2+(-7)2
=74,
故答案为:74.
∴两式相加得:a-c=-7,
∴(a-b)2+(b-c)2+(a-c)2
=(-3)2+(-4)2+(-7)2
=74,
故答案为:74.
点评:本题考查了求出代数式的值的应用,主要考查学生的计算能力,用了整体代入思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果抛物线y=x2+2向右平移1个单位长度,那么所得新抛物线的解析式为( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+2 |
| C、y=x2+3 |
| D、y=x2+1 |
已知
=
,那么下列式子中一定成立的是( )
| m |
| 3 |
| n |
| 4 |
| A、4m=3n | B、3m=4n |
| C、m=4n | D、mn=12 |
 如图的几何体中,它的俯视图是( )
如图的几何体中,它的俯视图是( )A、 |
B、 |
C、 |
D、 |
比-1大的数是( )
| A、-3 | ||
| B、0 | ||
C、-
| ||
| D、-1 |
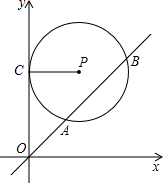 如图,在平面直角坐标系xOy中,⊙P与y轴相切于点C,⊙P的半径是4,直线y=x被⊙P截得的弦AB的长为
如图,在平面直角坐标系xOy中,⊙P与y轴相切于点C,⊙P的半径是4,直线y=x被⊙P截得的弦AB的长为