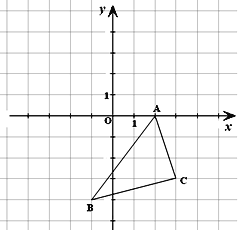
题目内容
【题目】已知![]() ,
,![]() 是直线
是直线![]() 上的点,
上的点,![]() .
.
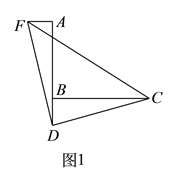
(![]() )如图
)如图![]() ,过点
,过点![]() 作
作![]() ,并截取
,并截取![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,判断
,判断![]() 的形状并证明.
的形状并证明.
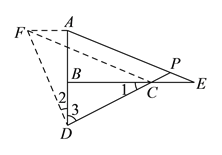
(![]() )如图
)如图![]() ,
,![]() 是直线
是直线![]() 上的一点,直线
上的一点,直线![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() ,求证
,求证![]() .
.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)利用SAS证明![]() ≌
≌![]() ,利用全等三角形的性质得出
,利用全等三角形的性质得出![]() ,即可判断三角形的形状;
,即可判断三角形的形状;
(2)过点![]() 作
作![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,就可以得出
,就可以得出![]() ≌
≌![]() ,就有
,就有![]() ,
,![]() ,就可以得出
,就可以得出![]() 为等腰直角三角形,就有
为等腰直角三角形,就有![]() ,就有
,就有![]() ∥
∥![]() ,进而得到
,进而得到![]() ∥
∥![]() 就可以得出四边形
就可以得出四边形![]() 是平行四边形,就有
是平行四边形,就有![]() .
.
试题解析:(![]() )
)![]() 是等腰直角三角形,
是等腰直角三角形,
证明:∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.
(![]() )证明:过点
)证明:过点![]() 作
作![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ∥
∥![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ∥
∥![]()
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目