��Ŀ����
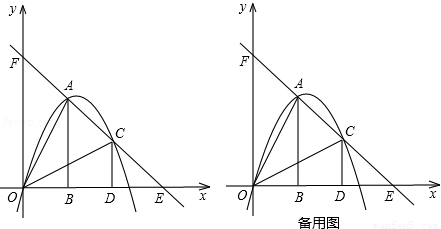
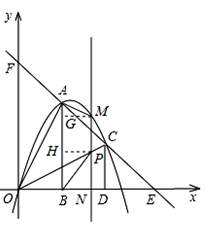
��ͼ��������ȫ�ȵ�Rt��AOB��Rt��COD�ֱ�����ƽ��ֱ������ϵ�У�ʹֱ�DZ�OB��OD��x���ϣ���֪��A��1��2������A��C�����ֱ�߷ֱ�x�ᡢy���ڵ�E��F��������y=ax2+bx+c����O��A��C���㣮
��1����������ߵĺ�������ʽ��
��2����PΪ�߶�OC��һ�����㣬����P��y���ƽ���߽��������ڵ�M����x���ڵ�N�����Ƿ���������ĵ�P��ʹ���ı���ABPMΪ�������Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������AOB��AC����ƽ�ƣ���Aʼ�����߶�AC�ϣ��Ҳ����C�غϣ�����AOB��ƽ�ƹ����� ���COD�ص����������ΪS����̽��S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
���COD�ص����������ΪS����̽��S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��1����������ߵĺ�������ʽ��
��2����PΪ�߶�OC��һ�����㣬����P��y���ƽ���߽��������ڵ�M����x���ڵ�N�����Ƿ���������ĵ�P��ʹ���ı���ABPMΪ�������Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������AOB��AC����ƽ�ƣ���Aʼ�����߶�AC�ϣ��Ҳ����C�غϣ�����AOB��ƽ�ƹ�����
 ���COD�ص����������ΪS����̽��S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
���COD�ص����������ΪS����̽��S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�⣺��1����������y=ax2+bx+c������O��A��C���ɵ�c=0��
��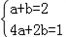 ��
��
���a=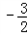 ��b=
��b= ��
��
�������߽���ʽΪy=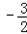 x2+
x2+ x��
x��
��2�����P�ĺ�����Ϊt����PN��CD��
���OPN�ס�OCD���ɵ�PN=
��P��t�� ����
����
�ߵ�M���������ϣ���M��t��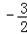 t2+
t2+ t����
t����
��ͼ�٣���M����MG��AB��G����P ����PH��AB��H��
����PH��AB��H��
AG=yA��yM=2����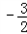 t2+
t2+ t��=
t��= t2��
t2�� t+2��
t+2��
BH=PN= ��
��
��AG=BHʱ���ı���ABPMΪ�������Σ�
�� t2��
t2�� t+2=
t+2= �������3t2��8t+4=0��
�������3t2��8t+4=0��
���t1=2���������⣬��ȥ����t2= ��
��
���P�������� ��
�� ��
��
����ڵ�P�� ��
�� ����ʹ���ı���ABPMΪ�������Σ�
����ʹ���ı���ABPMΪ�������Σ�
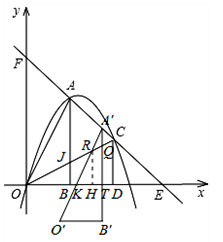
��3����ͼ�ڣ���AOB��AC����ƽ������A��O��B�䣬A��B�佻x����T����OC��Q��A��O�佻x����K����OC��R��
��ù�A��C��ֱ��ΪyAC=��x+3�������A��ĺ�����Ϊa��
���A�䣨a����a+3������֪��OQT�ס�OCD��
�ɵ�QT= �����Q������Ϊ��a��
�����Q��������a�� ����
����
�ⷨһ����AB��OC�ཻ�ڵ�J��
�ߡ�ARQ�ס�AOJ�����������ζ�Ӧ�ߵıȵ������Ʊȣ�
��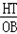 =
=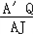 ��HT=
��HT=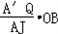 =
=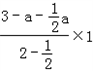 =2��a��KT=
=2��a��KT= A��T=
A��T= ��3��a����
��3��a����
A��Q=yA�䩁yQ=����a+3���� =3��
=3�� a��
a��
S�ı���RKTQ=S��A��KT��S��A��RQ= KT?A��T��
KT?A��T�� A��Q?HT
A��Q?HT
=
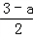 ��3��a����
��3��a���� ��3��
��3�� a������a+2��
a������a+2��
=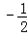 a2+
a2+ a��
a�� =
=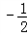 ��a��
��a�� ��2+
��2+ ����
����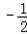 ��0��
��0��
�����߶�AC�ϴ��ڵ�A�䣨 ��
�� ����
����
��ʹ�ص��������Sȡ�����ֵ�����ֵΪ ��
��
�ⷨ��������R��RH��x����H�����ɡ�ORH�ס�OCD��
��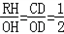 ���ɡ�RKH�ס�A��O��B�䣬��
���ɡ�RKH�ס�A��O��B�䣬��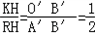 ��
��
�ɢ٣��ڵ�KH= OH��OK=
OH��OK= OH��KT=OT��OK=a��
OH��KT=OT��OK=a�� OH
OH
���ɡ�A��KT�ס�A��O��B�䣬��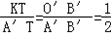 ����KT=
����KT=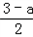 ��
��
�ɢۣ��ܵ�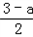 =a��
=a�� OH����OH=2a��2��RH=a��1��
OH����OH=2a��2��RH=a��1��
���Ե�R������ΪR��2a��2��a��1��
S�ı���RKTQ=S��QOT��S��ROK= OT?QT��
OT?QT�� OK?RH=
OK?RH= a?
a? a��
a�� ��1+
��1+ a��
a�� ����a��1��
����a��1��
=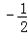 a2+
a2+ a��
a�� =
=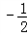 ��a��
��a�� ��2+
��2+ ����
����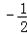 ��0��
��0��
�����߶�AC�ϴ��ڵ�A�䣨 ��
�� ����
����
��ʹ�ص��������Sȡ�����ֵ�����ֵΪ ��
��
�ⷨ������AB=2��OB=1��
��tan��O��A��B��=tan��OAB= ��
��
��KT=A��T?tan��O��A��B��=����a+3�� =
=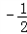 a+
a+ ��
��
��OK=OT��KT=a����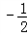 a+
a+ ��=
��= a��
a�� ��
��
����R��RH��x����H��
��tan��OAB=tan��RKH=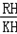 =2��
=2��
��RH=2KH
�֡�tan��OAB=tan��ROH=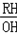 =
=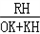 =
= ��
��
��2RH=OK+KH= a��
a�� +
+ RH��
RH��
��RH=a��1��OH=2��a��1����
���R����R��2a��2��a��1��S�ı���RKTQ=S��A��KT��S��A��RQ= KT?A��T��
KT?A��T�� A��Q��xQ��xR��=
A��Q��xQ��xR��=
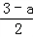 ��3��a����
��3��a���� ��3��
��3�� a������a+2��
a������a+2��
=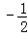 a2+
a2+ a��
a�� =
=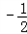 ��a��
��a�� ��2+
��2+ ����
����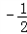 ��0��
��0��
�����߶�AC�ϴ��ڵ�A�䣨 ��
�� ����
����
��ʹ�ص��������Sȡ�����ֵ�����ֵΪ ��
��
��
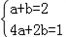 ��
�����a=
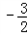 ��b=
��b= ��
���������߽���ʽΪy=
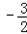 x2+
x2+ x��
x����2�����P�ĺ�����Ϊt����PN��CD��
���OPN�ס�OCD���ɵ�PN=

��P��t��
 ����
�����ߵ�M���������ϣ���M��t��
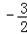 t2+
t2+ t����
t������ͼ�٣���M����MG��AB��G����P
 ����PH��AB��H��
����PH��AB��H��AG=yA��yM=2����
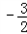 t2+
t2+ t��=
t��= t2��
t2�� t+2��
t+2��BH=PN=
 ��
����AG=BHʱ���ı���ABPMΪ�������Σ�
��
 t2��
t2�� t+2=
t+2= �������3t2��8t+4=0��
�������3t2��8t+4=0�����t1=2���������⣬��ȥ����t2=
 ��
�����P��������
 ��
�� ��
������ڵ�P��
 ��
�� ����ʹ���ı���ABPMΪ�������Σ�
����ʹ���ı���ABPMΪ�������Σ���3����ͼ�ڣ���AOB��AC����ƽ������A��O��B�䣬A��B�佻x����T����OC��Q��A��O�佻x����K����OC��R��
��ù�A��C��ֱ��ΪyAC=��x+3�������A��ĺ�����Ϊa��
���A�䣨a����a+3������֪��OQT�ס�OCD��
�ɵ�QT=
 �����Q��������a��
�����Q��������a�� ����
�����ⷨһ����AB��OC�ཻ�ڵ�J��
�ߡ�ARQ�ס�AOJ�����������ζ�Ӧ�ߵıȵ������Ʊȣ�
��
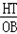 =
=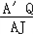 ��HT=
��HT=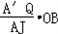 =
=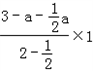 =2��a��KT=
=2��a��KT= A��T=
A��T= ��3��a����
��3��a����A��Q=yA�䩁yQ=����a+3����
 =3��
=3�� a��
a��S�ı���RKTQ=S��A��KT��S��A��RQ=
 KT?A��T��
KT?A��T�� A��Q?HT
A��Q?HT=

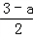 ��3��a����
��3��a���� ��3��
��3�� a������a+2��
a������a+2��=
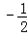 a2+
a2+ a��
a�� =
=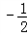 ��a��
��a�� ��2+
��2+ ����
����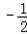 ��0��
��0�������߶�AC�ϴ��ڵ�A�䣨
 ��
�� ����
������ʹ�ص��������Sȡ�����ֵ�����ֵΪ
 ��
���ⷨ��������R��RH��x����H�����ɡ�ORH�ס�OCD��
��
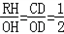 ���ɡ�RKH�ס�A��O��B�䣬��
���ɡ�RKH�ס�A��O��B�䣬��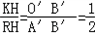 ��
���ɢ٣��ڵ�KH=
 OH��OK=
OH��OK= OH��KT=OT��OK=a��
OH��KT=OT��OK=a�� OH
OH ���ɡ�A��KT�ס�A��O��B�䣬��
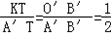 ����KT=
����KT=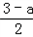 ��
���ɢۣ��ܵ�
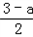 =a��
=a�� OH����OH=2a��2��RH=a��1��
OH����OH=2a��2��RH=a��1�����Ե�R������ΪR��2a��2��a��1��
S�ı���RKTQ=S��QOT��S��ROK=
 OT?QT��
OT?QT�� OK?RH=
OK?RH= a?
a? a��
a�� ��1+
��1+ a��
a�� ����a��1��
����a��1��=
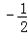 a2+
a2+ a��
a�� =
=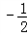 ��a��
��a�� ��2+
��2+ ����
����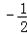 ��0��
��0�������߶�AC�ϴ��ڵ�A�䣨
 ��
�� ����
������ʹ�ص��������Sȡ�����ֵ�����ֵΪ
 ��
���ⷨ������AB=2��OB=1��
��tan��O��A��B��=tan��OAB=
 ��
����KT=A��T?tan��O��A��B��=����a+3��
 =
=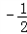 a+
a+ ��
����OK=OT��KT=a����
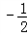 a+
a+ ��=
��= a��
a�� ��
������R��RH��x����H��
��tan��OAB=tan��RKH=
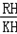 =2��
=2����RH=2KH
�֡�tan��OAB=tan��ROH=
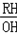 =
= =
= ��
����2RH=OK+KH=
 a��
a�� +
+ RH��
RH����RH=a��1��OH=2��a��1����
���R����R��2a��2��a��1��S�ı���RKTQ=S��A��KT��S��A��RQ=
 KT?A��T��
KT?A��T�� A��Q��xQ��xR��=
A��Q��xQ��xR��=
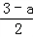 ��3��a����
��3��a���� ��3��
��3�� a������a+2��
a������a+2��=
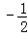 a2+
a2+ a��
a�� =
=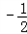 ��a��
��a�� ��2+
��2+ ����
����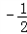 ��0��
��0�������߶�AC�ϴ��ڵ�A�䣨
 ��
�� ����
������ʹ�ص��������Sȡ�����ֵ�����ֵΪ
 ��
��
�� ��

��ϰ��ϵ�д�
�����Ŀ
 ���㣮
���㣮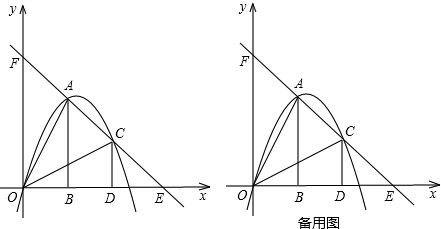
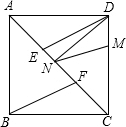
 ��2013•ʯ��ɽ��һģ����ͼ��������ȫ�ȵ�Rt��AOB��Rt��ECD�ֱ�����ƽ��ֱ������ϵxOy�У�ʹ��E���B�غϣ�ֱ�DZ�OB��BC��y���ϣ���֪��D ��4��2������A��D�����ֱ�߽�y���ڵ�F������ECD��DA������ÿ��
��2013•ʯ��ɽ��һģ����ͼ��������ȫ�ȵ�Rt��AOB��Rt��ECD�ֱ�����ƽ��ֱ������ϵxOy�У�ʹ��E���B�غϣ�ֱ�DZ�OB��BC��y���ϣ���֪��D ��4��2������A��D�����ֱ�߽�y���ڵ�F������ECD��DA������ÿ��