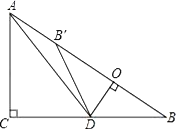
题目内容
【题目】在等边![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 边上一动点,
边上一动点,![]() ,且
,且![]() 的两边分别与
的两边分别与![]() 的边
的边![]() ,
,![]() 交于点
交于点![]() ,
,![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合).
重合).
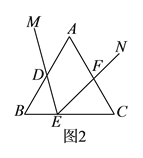
(![]() )当
)当![]() 时,请在图
时,请在图![]() 中补全图形.
中补全图形.
(![]() )在图
)在图![]() 中,设
中,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
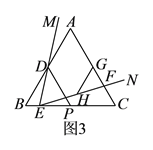
(![]() )如图
)如图![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,在
的中点,在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,![]() .请证明
.请证明![]() .
.
【答案】(![]() )见解析.(
)见解析.(![]() )
)![]() .(
.(![]() )见解析
)见解析
【解析】试题分析:(1)根据题意,画出图形即可;(2)根据已知条件证明![]() 根据相似三角形的性质即可求得
根据相似三角形的性质即可求得![]() 与
与![]() 的函数关系式;(3)根据已知条件先证得△DEH为等边三角形,可得DE=DH=EH,利用SAS证明△DEP≌△DHG,由∠DEP=∠HFG,∠HGF=∠EDH =60°,即可判定△DEP∽△HFG.
的函数关系式;(3)根据已知条件先证得△DEH为等边三角形,可得DE=DH=EH,利用SAS证明△DEP≌△DHG,由∠DEP=∠HFG,∠HGF=∠EDH =60°,即可判定△DEP∽△HFG.
试题解析:
(![]() )如图.
)如图.

(![]() )∵
)∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,则
,则![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

(![]() )连接DH、DG,
)连接DH、DG,
∵![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案【题目】我们约定:体重在选定标准的![]() %(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
%(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
体重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根据以上表格信息解决如下问题:
(1)将这组数据的三个统计量:平均数、中位数和众数填入下表:
平均数 | 中位数 | 众数 |
(2)请你选择其中一个统计量作为选定标准,说明选择的理由.并按此选定标准找出这10名男生中具有“一般体重”的男生.
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?