题目内容
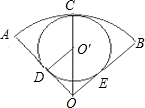如图，已知扇形OACB中，∠AOB=120°，弧AB长为L=4π，⊙O′和弧AB，OA，OB分别相切于点C，D，E，求⊙O′的周长．
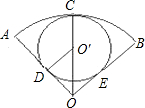解：∵∠AOB=120°，弧AB长为L=4π，∴4π=
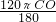，∴OC=6，
∴OO′=6-CO′=6-DO′，
∵⊙O′和弧AB，OA，OB分别相切于点C，D，E，
∴∠O′DO=90°，∠DOO′=
∠AOB=60°，∴sin60°=
=
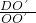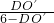，∴DO′=12
-18，∴⊙O′的周长为：2（12
-18）π．分析：先求得OC=6，OO′=6-CO′=6-DO′，再利用解直角三角形求出圆的半径，从而求得⊙O′的周长．
点评：此题考查了弧长公式：l=
以及圆的切线的性质等知识，根据已知得出sin60°=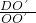=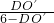是解题关键． 
练习册系列答案
相关题目
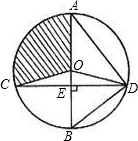如图，已知⊙O的直径AB垂直于弦CD于E，连接AD、BD、OC、OD，且OD=5．
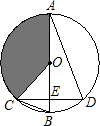如图，已知⊙O的直径AB垂直弦CD于点E，连接AD、BC、OC，且OC=5．
如图，已知⊙O的直径AB垂直于弦CD于E，连接AD、BD、OC、OD，且OD=5．
，求CD的长；
，求CD的长；