题目内容
如图,直径AE平分弦CD,交CD于点G,EF∥CD,交AD的延长线于F,AP⊥AC交CD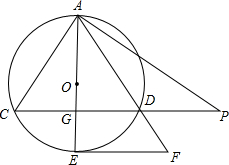 的延长线于点P.
的延长线于点P.(1)求证:EF是⊙O的切线;
(2)若AC=2,PD=
| 1 | 2 |
分析:(1)欲证明EF是⊙O的切线,只需证明∠AEF=90°即可;
(2)利用相似三角形的判定定理AA证得△CAG∽△CPA,然后由相似三角形的对应边成比例知AC2=CG•CP,从而求得CP2=12;再在直角三角形APC中利用勾股定理求得AP的长度;最后由直角三角形中的锐角三角函数的定义求得tan∠P的值.
(2)利用相似三角形的判定定理AA证得△CAG∽△CPA,然后由相似三角形的对应边成比例知AC2=CG•CP,从而求得CP2=12;再在直角三角形APC中利用勾股定理求得AP的长度;最后由直角三角形中的锐角三角函数的定义求得tan∠P的值.
解答:(1)证明:∵直径AE平分弦CD,
∴AG⊥CD(垂径定理).(3分)
∵EF∥CD(已知),
∴∠AEF=∠AGD=90°.
∴EF是⊙O的切线.(6分)
(2)∵∠CAP=∠AGC=90°,∠ACG=∠PCA.
∴△CAG∽△CPA(AA).
∴AC2=CG•CP(相似三角形的对应边成比例).(9分)
又∵PD=
CD(已知),
CG=GD,
∴CG=
PC.而AC=2,
∴22=
PC•PC,∴PC2=12.(11分)
又∵AC⊥AP,∴AP2=PC2-AC2(勾股定理),
∴AP=2
.(13分)
∴tan∠P=
=
=
.(15分)
∴AG⊥CD(垂径定理).(3分)
∵EF∥CD(已知),
∴∠AEF=∠AGD=90°.
∴EF是⊙O的切线.(6分)
(2)∵∠CAP=∠AGC=90°,∠ACG=∠PCA.
∴△CAG∽△CPA(AA).
∴AC2=CG•CP(相似三角形的对应边成比例).(9分)
又∵PD=
| 1 |
| 2 |
CG=GD,
∴CG=
| 1 |
| 3 |
∴22=
| 1 |
| 3 |
又∵AC⊥AP,∴AP2=PC2-AC2(勾股定理),
∴AP=2
| 2 |
∴tan∠P=
| AC |
| AP |
| 2 | ||
2
|
| ||
| 2 |
点评:本题考查了相似三角形的判定定理、切线的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
 (2012•柳州)如图,AB是⊙O的直径,AC是弦.
(2012•柳州)如图,AB是⊙O的直径,AC是弦.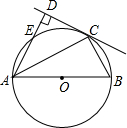 如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,且AE⊥CP于点D,且AC平分∠DAB.
如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,且AE⊥CP于点D,且AC平分∠DAB. 的延长线于点P.
的延长线于点P. CD,求tan∠P的值.
CD,求tan∠P的值. CD,求tan∠P的值.
CD,求tan∠P的值.