题目内容
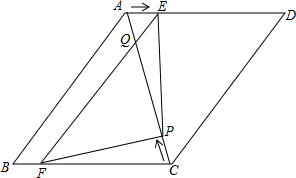
如图，五边形ABCDE中，BC=DE，AE=DC，DM是AB的垂直平分线．证明：∠E=∠C．分析：利用全等三角形的判定定理SSS证得△ADE≌△DBC，然后利用全等三角形的对应角相等证得结论．
解答：
证明：如图，连接AD、BD．
∵DM是AB的垂直平分线（已知），
∴AD=BD（线段垂直平分线上的点到线段两端的距离相等）．
在△ADE与△DBC中，
，
∴△ADE≌△DBC（SSS），
∴∠E=∠C（全等三角形的对应角相等）．
证明：如图，连接AD、BD．∵DM是AB的垂直平分线（已知），
∴AD=BD（线段垂直平分线上的点到线段两端的距离相等）．
在△ADE与△DBC中，
|
∴△ADE≌△DBC（SSS），
∴∠E=∠C（全等三角形的对应角相等）．
点评：本题考查了全等三角形的判定与性质，线段垂直平分线的性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
练习册系列答案
名校课堂系列答案
相关题目
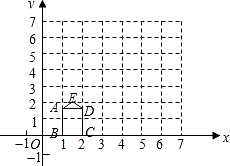如图，矩形ABCD的长，宽分别为
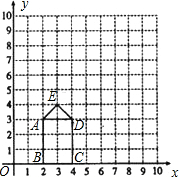如图，矩形ABCD的长、宽分别为3和2，OB=2，点E的坐标为（3，4）连接AE、ED．
如图，四边形ABCD的内角和为2×180°=360°，五边形ABCDE的内角和为3×180°=540°，…由此可见：