题目内容
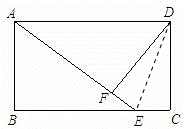
在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F；
求证：DF=DC．
考点：
矩形的性质；全等三角形的判定与性质．
专题：
证明题．
分析：
根据矩形的性质和DF⊥AE于F，可以得到∠DEC=∠AED，∠DFE=∠C=90，进而依据AAS可以证明△DFE≌△DCE．然后利用全等三角形的性质解决问题．
解答：
证明：连接DE．（1分）
∵AD=AE，
∴∠AED=∠ADE．（1分）
∵有矩形ABCD，
∴AD∥BC，∠C=90°．（1分）
∴∠ADE=∠DEC，（1分）
∴∠DEC=∠AED．
又∵DF⊥AE，
∴∠DFE=∠C=90°．
∵DE=DE，（1分）
∴△DFE≌△DCE．
∴DF=DC．（1分）
点评：
此题比较简单，主要考查了矩形的性质，全等三角形的性质与判定，综合利用它们解题．
练习册系列答案
相关题目
1、如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F．线段DF与图中的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．即DF=AB
．（写出一条线段即可）
14、如图所示，在矩形ABCD中，点E在BC上，AE=AD，DF⊥AE于F，若AB=3，BC=5，则四边形DFEC的面积是（ ）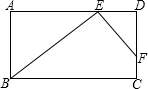
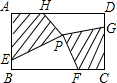如图，在矩形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，点P在矩形ABCD内，若AB=4，BC=6，AE=CG=3，BF=DH=4，四边形AEPH的面积为5，求四边形PFCG的面积．
（2013•泰州）如图，在矩形ABCD中，点P在边CD上，且与C、D不重合，过点A作AP的垂线与CB的延长线相交于点Q，连接PQ，M为PQ中点．