Question

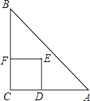
【题目】如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分的面积为（结果保留π）（ ）

A.
B.
C.
D.16

Answer 1

【答案】C
【解析】连接AD，OD，

∵等腰直角△ABC中，
∴∠ABD=45°．
∵AB是圆的直径，
∴∠ADB=90°，
∴△ABD也是等腰直角三角形，
∴ ．
∵AB=8，
∴AD=BD=4 ，
∴S阴影=S△ABC-S△ABD-S弓形AD
=S△ABC-S△ABD-（S扇形AOD- S△ABD）
= ×8×8- ×4 ×4 - + × ×4 ×4
=16-4π+8
=24-4π．
所以答案是：C.
【考点精析】根据题目的已知条件，利用扇形面积计算公式的相关知识可以得到问题的答案，需要掌握在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．