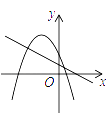题目内容
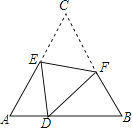
【题目】如图1,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 和点
和点![]() 关于原点对称,点
关于原点对称,点![]() 是直线
是直线![]() 位于
位于![]() 轴右侧部分图象上一点,连接
轴右侧部分图象上一点,连接![]() ,已知
,已知![]() .
.
(1)求直线![]() 的解析式;
的解析式;
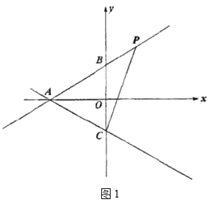
(2)如图2,![]() 沿着直线
沿着直线![]() 平移得
平移得![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合.点
重合.点![]() 为直线
为直线![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出
的值最小时,请求出![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
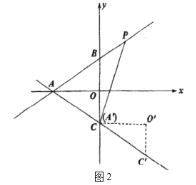
(3)如图3,将![]() 沿直线
沿直线![]() 是翻折得
是翻折得![]() 点
点![]() 为平面内任意一动点,在直线
为平面内任意一动点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使得以点
,使得以点![]() 为顶点的四边形是矩形;若存在,请直接写出点
为顶点的四边形是矩形;若存在,请直接写出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)![]() ;
;
(2)点![]() ,
,![]() ,
,![]() 最小值
最小值![]() ;
;
(3)点![]() ,
,![]() 或
或![]() ,
,![]() .
.
【解析】
(1)点![]() 和点
和点![]() 关于原点对称,则点
关于原点对称,则点![]() ,将点
,将点![]() 、
、![]() 的坐标代入一次函数表达式,即可求解;
的坐标代入一次函数表达式,即可求解;
(2)过点![]() 作直线
作直线![]() 轴,过点
轴,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,即此时,
,即此时,![]() 最小,最小值为
最小,最小值为![]() ,即可求解;
,即可求解;
(3)点![]() 、
、![]() 均在直线
均在直线![]() 上,而
上,而![]() 与
与![]() 不垂直,故点
不垂直,故点![]() 不可能是矩形的边,只能是矩形的对角线,即可求解.
不可能是矩形的边,只能是矩形的对角线,即可求解.
解:(1)点![]() 和点
和点![]() 关于原点对称,则点
关于原点对称,则点![]() ,
,
将点![]() 、
、![]() 的坐标代入一次函数表达式:
的坐标代入一次函数表达式:![]() 得:
得:![]() ,解得:
,解得: ,
,
故直线![]() 的表达式为:
的表达式为:![]() ;
;

(2)过点![]() 作直线
作直线![]() 轴,过点
轴,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,
,
![]() ,故
,故![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
则![]() ,即此时,
,即此时,![]() 最小,最小值为
最小,最小值为![]() ,
,
![]() ,则
,则![]() ,
,
故点![]() ,
,![]() ,
,
![]() ,则点
,则点![]() ,
,![]() ,
,
则点![]() ,
,![]() ,
,
点![]() ,
,![]() ,
,
![]() 最小值
最小值![]() ;
;

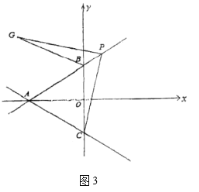
(3)存在,理由:
①当![]() 时,
时,
如图![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,
故点![]() ,
,![]() ;
;
![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形,
为顶点的四边形是矩形,
点![]() 位置如下图所示,设点
位置如下图所示,设点![]() ,
,
将点![]() 、
、![]() 的坐标代入一次函数:
的坐标代入一次函数:![]() 得:
得:![]() ,解得:
,解得: ,
,
故直线![]() 的表达式为:
的表达式为:![]() ①,
①,
![]() ,则设直线
,则设直线![]() 的表达式为:
的表达式为:![]() ,
,
将点![]() 的坐标代入上式得:
的坐标代入上式得:![]() ,解得:
,解得:![]() ,
,
故:直线![]() 的表达式为:
的表达式为:![]() ②,
②,
联立①②并解得:![]() ,
,
故点![]() ,
,![]() ;
;
②当![]() 时,
时,
同理可得:点![]() ,
,![]() ;
;

综上所述,点![]() ,
,![]() 或
或![]() ,
,![]() .
.

练习册系列答案
相关题目