题目内容
2.化简求值:[$\frac{x+2}{x(x-1)}$-$\frac{1}{x-1}$]•$\frac{x}{x-1}$,其中x=$\sqrt{2}$+1.分析 首先将中括号内的部分进行通分,然后按照同分母分式的减法法则进行计算,再按照分式的乘法法则计算、化简,最后再代数求值即可.
解答 解:原式=$[\frac{x+2}{x(x-1)}-\frac{x}{x(x-1)}]•\frac{x}{x-1}$
=$\frac{2}{x(x-1)}•\frac{x}{x-1}$
=$\frac{2}{(x-1)^{2}}$,
将x=$\sqrt{2}$+1代入得:原式=$\frac{2}{(\sqrt{2}+1-1)^{2}}$=$\frac{2}{(\sqrt{2})^{2}}=\frac{2}{2}=1$.
点评 本题主要考查的是分式的化简以及二次根式的运算,掌握分式的通分、加减、乘除等运算法则是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.3的倒数是( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
10.某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
| 类别/单价 | 成本价 | 销售价(元/箱) |
| 甲 | 24 | 36 |
| 乙 | 33 | 48 |
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
17.为加快新农村试点示范建设,我省开展了“美丽乡村”的评选活动,下表是我省六个州(市)推荐候选的“美丽乡村”个数统计结果:
在上表统计的数据中,平均数和中位数分别为( )
| 州(市) | A | B | C | D | E | F |
| 推荐数(个) | 36 | 27 | 31 | 56 | 48 | 54 |
| A. | 42,43.5 | B. | 42,42 | C. | 31,42 | D. | 36,54 |
7.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为S甲2=0.51,S乙2=0.41、S丙2=0.62、S丁2=0.45,则四人中成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
20.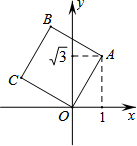 如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
 如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )| A. | ($\sqrt{3}$,1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (-$\sqrt{3}$,-1) |
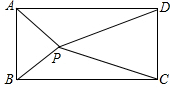 如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2.
如图,四边形ABCD是长方形,点P是长方形内的任意一点,求证:PA2+PC2=PB2+PD2.