题目内容
小阳遇到这样一个问题:如图(1),O为等边△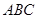 内部一点,且
内部一点,且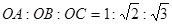 ,求
,求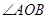 的度数.
的度数.
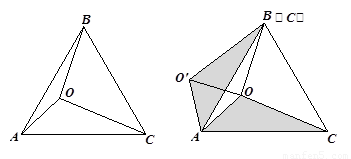

|
小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△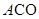 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△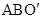 ,连结
,连结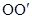 . 则△
. 则△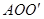 是等边三角形,故
是等边三角形,故 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形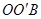 中.
中.
1.请你回答: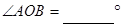 .
.
2.参考小阳思考问题的方法,解决下列问题:
已知:如图(3),四边形ABCD中,AB=AD,∠DAB=60°,∠DCB=30°,AC=5,CD=4.求四边形ABCD的面积.
1.150°
2.如图,将△ 绕点
绕点 顺时针旋转60°,使点D与点B重合,………2分
顺时针旋转60°,使点D与点B重合,………2分
得到△ ,连结
,连结 . 则△
. 则△ 是等边三角形,
是等边三角形,

可知 ,
, ……………………3分
……………………3分
在四边形ABCD中, ,
,

 .
……………………4分
.
……………………4分

 .………………5分
.………………5分
【解析】(1)经旋转后得出三角形OO′B是直角三角形,从而得出 的度数;
的度数;
(2)将△ 绕点
绕点 顺时针旋转60°然后得出O′BC是直角三角形,利用勾股定理求出BC的长,利用
顺时针旋转60°然后得出O′BC是直角三角形,利用勾股定理求出BC的长,利用 求出结果。
求出结果。

 阅读快车系列答案
阅读快车系列答案小阳遇到这样一个问题:如图(1),O为等边△![]() 内部一点,且
内部一点,且![]() ,求
,求![]() 的度数.
的度数.

|
小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△![]() 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△![]() ,连结
,连结![]() . 则△
. 则△![]() 是等边三角形,故
是等边三角形,故![]() ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形![]() 中.
中.
1.请你回答:![]() .
.
2.参考小阳思考问题的方法,解决下列问题:
已知:如图(3),四边形ABCD中,AB=AD,∠DAB=60°,∠DCB=30°,AC=5,CD=4.求四边形ABCD的面积.
 内部一点,且
内部一点,且 ,求
,求 的度数.
的度数.

|
小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△
 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△ ,连结
,连结 . 则△
. 则△ 是等边三角形,故
是等边三角形,故 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形 中.
中.【小题1】请你回答:
 .
.【小题2】参考小阳思考问题的方法,解决下列问题:
已知:如图(3),四边形ABCD中,AB=AD,∠DAB=60°,∠DCB=30°,AC=5,CD=4.求四边形ABCD的面积.
小阳遇到这样一个问题:如图(1),O为等边△ 内部一点,且
内部一点,且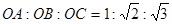 ,求
,求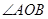 的度数.
的度数.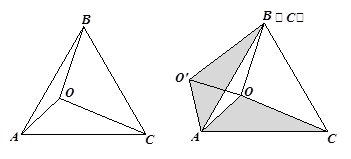
|
小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△
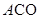 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△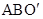 ,连结
,连结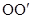 . 则△
. 则△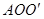 是等边三角形,故
是等边三角形,故 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形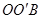 中.
中.【小题1】请你回答:
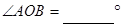 .
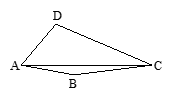
.【小题2】参考小阳思考问题的方法,解决下列问题:
已知:如图(3),四边形ABCD中,AB=AD,∠DAB=60°,∠DCB=30°,AC=5,CD=4.求四边形ABCD的面积.
