题目内容
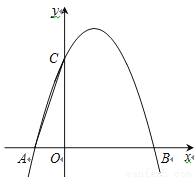
如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.
(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
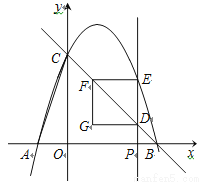
练习册系列答案
相关题目


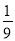 B.
B. 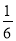 C.
C. 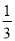 D.
D. 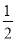
 的图像上,则( )
的图像上,则( )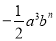 是同类项,则m+n=__________.
是同类项,则m+n=__________.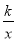 图象上.
图象上.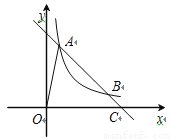
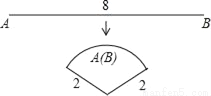

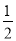 AB时,求t的值.
AB时,求t的值.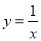 ,下列结论中不正确的是( )
,下列结论中不正确的是( )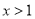 时,
时, 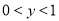 D. 当
D. 当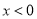 时,y随着x的增大而增大
时,y随着x的增大而增大