题目内容
平面直角坐标系中，已知A、B两点的坐标分别为A（-2，3）、B（1，2），点P为x轴上一动点，当P到A、B两点的距离之和最小时，求点P的坐标．
解：依题意得：
B（1，2）关于x轴的对称点是（1，-2）
过A（-2，3）与（1，-2）的直线为y=kx+b
∴
，
∴
，
∴y=-
x-
，
令y=0，得x=-
．
故P点坐标为（-，0）．
分析：本题根据题意可知B（1，2）关于x轴的对称点是（1，-2），经过A（-2，3）与（1，-2）的直线可以求出，这条直线与x轴的交点就是P点．
点评：此题考查了最短线路问题及坐标与图形的性质；能够正确作出P点的位置是解决本题的关键．
B（1，2）关于x轴的对称点是（1，-2）
过A（-2，3）与（1，-2）的直线为y=kx+b
∴
，∴
，∴y=-
x-，令y=0，得x=-
．故P点坐标为（-
，0）．分析：本题根据题意可知B（1，2）关于x轴的对称点是（1，-2），经过A（-2，3）与（1，-2）的直线可以求出，这条直线与x轴的交点就是P点．
点评：此题考查了最短线路问题及坐标与图形的性质；能够正确作出P点的位置是解决本题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
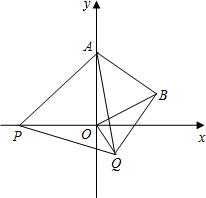一边，在其一侧作等边三角形APQ．当点P运动到原点O处时，记Q的位置为B．
21、如图，在平面直角坐标系中，已知点A坐标为（2，4），直线x=2与x轴相交于点B，连接OA，抛物线y=x2从点O沿OA方向平移，与直线x=2交于点P，顶点M到A点时停止移动．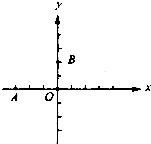
18、如图，在平面直角坐标系中，已知平行四边形的三个顶点坐标分别是O（0，0），A（-3，0），B（0，2），求平行四边形第四个顶点C的坐标．
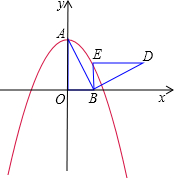出M在抛物线内部（指抛物线与X轴所围成的部分）时t的取值范围．