Question

【题目】请阅读下列材料：

问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．

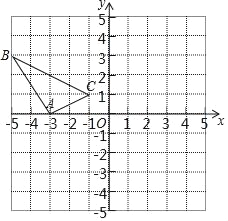
李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为，问题得到解决．

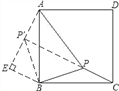
请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=，BP=，PC=1．求∠BPC度数的大小和正方形ABCD的边长．

Answer 1

【答案】（1）135°；（2）；

【解析】试题分析：

（1）如图，将△BPC绕点B逆时针旋转90°，得△BP′A，则△BPC≌△BP′A，由此可得：AP′=PC=1，BP=BP′=；连接PP′，由∠PBP′=90°可得PP′=2，∠BP′P=45°，这样在△AP′P中由勾股定理的逆定理可得∠AP′P=90°，从而可得∠AP′B=135°，由此可得∠BPC=∠AP′B=135°；

（2）过点B作BE⊥AP′，交AP′的延长线于点E，结合（1）中∠AP′B=135°可证得△BEP′是等腰直角三角形，结合BP′=，可得EP′=BE=1，从而可得AE=2，结合BE=1在Rt△ABE中由勾股定理即可求得AB的长.

试题解析：

（1）如图，

将△BPC绕点B逆时针旋转90°，得△BP′A，则△BPC≌△BP′A．

∴AP′=PC=1，BP=BP′=；

连接PP′，

在Rt△BP′P中，

∵BP=BP′=，∠PBP′=90°，

∴PP′=2，∠BP′P=45°；

在△AP′P中，AP′=1，PP′=2，AP=，

∵，即AP′2+PP′2=AP2；

∴△AP′P是直角三角形，即∠AP′P=90°，

∴∠AP′B=135°，

∴∠BPC=∠AP′B=135°．

（2）过点B作BE⊥AP′，交AP′的延长线于点E，

∴∠BEP′=90°，

∵∠AP′B=135°，

∴∠EP′B=45°，

∴△BEP′是等腰直角三角形，

∵BP′=，

∴EP′=BE=1，

∴AE=AP′+EP′=2；

∴在Rt△ABE中，由勾股定理，得AB=；

∴∠BPC=135°，正方形边长为．