题目内容
 已知在平面直角坐标系中,⊙O的半径是8,又B、A两点的坐标分别是(0,b)、(10,0).
已知在平面直角坐标系中,⊙O的半径是8,又B、A两点的坐标分别是(0,b)、(10,0).
(1)当b=10时,求经过B、A两点的直线解析式;
(2)⊙O与所求直线的位置关系是怎样的?说明判断的理由.
(3)当B点在y轴上运动时,直线AB与⊙O有哪几种位置关系?并求每种位置关系时b的取值范围(直接写结论).
解:(1)b=10时,设过AB两点的解析式为y=kx+b
∵A(10,0)B(0,10)
∴
∴ ∴y=-x+10
∴y=-x+10
(2)过O作OC⊥AB于点C
∵OA=OB=10,∴AB=10 ,OC=
,OC= AB=5
AB=5
∵R=8>OC所以此时直线与⊙O相交有两个交点
(3)有三种位置关系
当b=± 时,直线AB与⊙O相切
时,直线AB与⊙O相切
当- <b<
<b< 时 直线AB与⊙O相交
时 直线AB与⊙O相交
当b> 或b<-
或b<- 时 直线AB与⊙O相离
时 直线AB与⊙O相离
分析:(1)设过AB两点的解析式为y=kx+b,将A、B两点的坐标代入即可;
(2)要判断⊙O与所求直线的位置关系,只需比较圆心到直线的距离与半径的大小即可;
(3)直线AB与⊙O有相交、相切、相离三种关系,求出对应的b值即可.
点评:本题考查了直线与圆的位置关系,难度适中,注意掌握直线与圆的三种位置关系:相交、相切和相离.
∵A(10,0)B(0,10)
∴

∴
 ∴y=-x+10
∴y=-x+10 (2)过O作OC⊥AB于点C
∵OA=OB=10,∴AB=10
 ,OC=
,OC= AB=5
AB=5
∵R=8>OC所以此时直线与⊙O相交有两个交点
(3)有三种位置关系
当b=±
 时,直线AB与⊙O相切
时,直线AB与⊙O相切 当-
 <b<
<b< 时 直线AB与⊙O相交
时 直线AB与⊙O相交 当b>
 或b<-
或b<- 时 直线AB与⊙O相离
时 直线AB与⊙O相离 分析:(1)设过AB两点的解析式为y=kx+b,将A、B两点的坐标代入即可;
(2)要判断⊙O与所求直线的位置关系,只需比较圆心到直线的距离与半径的大小即可;
(3)直线AB与⊙O有相交、相切、相离三种关系,求出对应的b值即可.
点评:本题考查了直线与圆的位置关系,难度适中,注意掌握直线与圆的三种位置关系:相交、相切和相离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
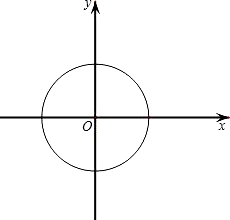 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.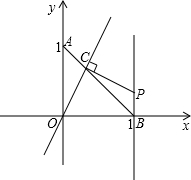 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.