题目内容
在等腰三角形中,∠A、∠B、∠C的对边分别为a、b、c,已知a=3,且b和c是方程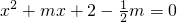 的两个实根,则△ABC的周长为
的两个实根,则△ABC的周长为
- A.7
- B.
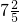
- C.6或11
- D.7或
D
分析:由b和c是方程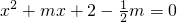 的两个实根,可得b+c=-m,bc=2-
的两个实根,可得b+c=-m,bc=2- m,△=m2-4(2-
m,△=m2-4(2- m)=m2+2m-8=(m+1)2-9≥0,然后分别从a=b,a=c或b=c去分析求解即可求得答案.
m)=m2+2m-8=(m+1)2-9≥0,然后分别从a=b,a=c或b=c去分析求解即可求得答案.
解答:∵b和c是方程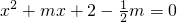 的两个实根,
的两个实根,
∴b+c=-m,bc=2- m,△=m2-4(2-
m,△=m2-4(2- m)=m2+2m-8=(m+1)2-9≥0,
m)=m2+2m-8=(m+1)2-9≥0,
若a=b=3,则3+c=-m,3c=2- m,
m,
解得: ,
,
∴此时△ABC的周长为:3+3+1 =7
=7 ;
;
同理:当a=c=3时,△ABC的周长为:3+3+1 =7
=7 ;
;
当b=c时,2b=m,b2=2- m,
m,
解得: ,
, ,
,
此时△ABC的周长为:2+2+3=7,
∵1+1<3,
∴不能组成三角形,舍去.
∴△ABC的周长为:7或7 .
.
故选:D.
点评:此题考查了根与系数的关系以及根的判别式.此题难度适中,注意掌握若二次项系数为1,x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.
分析:由b和c是方程
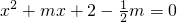 的两个实根,可得b+c=-m,bc=2-
的两个实根,可得b+c=-m,bc=2- m,△=m2-4(2-
m,△=m2-4(2- m)=m2+2m-8=(m+1)2-9≥0,然后分别从a=b,a=c或b=c去分析求解即可求得答案.
m)=m2+2m-8=(m+1)2-9≥0,然后分别从a=b,a=c或b=c去分析求解即可求得答案.解答:∵b和c是方程
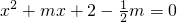 的两个实根,
的两个实根,∴b+c=-m,bc=2-
 m,△=m2-4(2-
m,△=m2-4(2- m)=m2+2m-8=(m+1)2-9≥0,
m)=m2+2m-8=(m+1)2-9≥0,若a=b=3,则3+c=-m,3c=2-
 m,
m,解得:
 ,
,∴此时△ABC的周长为:3+3+1
 =7
=7 ;
;同理:当a=c=3时,△ABC的周长为:3+3+1
 =7
=7 ;
;当b=c时,2b=m,b2=2-
 m,
m,解得:
 ,
, ,
,此时△ABC的周长为:2+2+3=7,
∵1+1<3,
∴不能组成三角形,舍去.
∴△ABC的周长为:7或7
 .
.故选:D.
点评:此题考查了根与系数的关系以及根的判别式.此题难度适中,注意掌握若二次项系数为1,x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
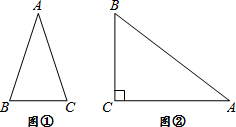 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=