题目内容
已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣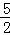 ).
).
(1)求抛物线l2的函数表达式;
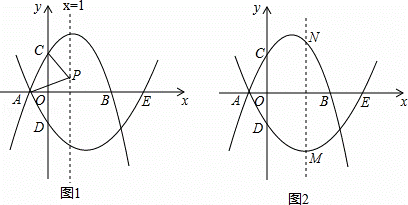
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1 于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
解:(1)∵抛物线l1:y=﹣x2+bx+3的对称轴为x=1,
∴﹣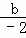 =1,解得b=2,
=1,解得b=2,
∴抛物线l1的解析式为y=﹣x2+2x+3,
令y=0,可得﹣x2+2x+3=0,解得x=﹣1或x=3,
∴A点坐标为(﹣1,0),
∵抛物线l2经过点A、E两点,
∴可设抛物线l2解析式为y=a(x+1)(x﹣5),
又∵抛物线l2交y轴于点D(0,﹣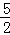 ),
),
∴﹣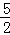 =﹣5a,解得a=
=﹣5a,解得a=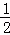 ,
,
∴y=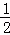 (x+1)(x﹣5)=
(x+1)(x﹣5)=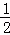 x2﹣2x﹣
x2﹣2x﹣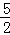 ,
,
∴抛物线l2的函数表达式为y= x2﹣2x﹣
x2﹣2x﹣ ;
;
(2)设P点坐标为(1,y),由(1)可得C点坐标为(0,3),
∴PC2=12+(y﹣3)2=y2﹣6y+10,PA2=[1﹣(﹣1)]2+y2=y2+4,
∵PC=PA,
∴y2﹣6y+10=y2+4,解得y=1,
∴P点坐标为(1,1);
(3)由题意可设M(x, x2﹣2x﹣
x2﹣2x﹣ ),
),
∵MN∥y轴,
∴N(x,﹣x2+2x+3), x2﹣2x﹣
x2﹣2x﹣
令﹣x2+2x+3= x2﹣2x﹣
x2﹣2x﹣ ,可解得x=﹣1或x=
,可解得x=﹣1或x=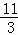 ,
,
①当﹣1<x≤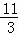 时,MN=(﹣x2+2x+3)﹣(
时,MN=(﹣x2+2x+3)﹣(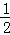 x2﹣2x﹣
x2﹣2x﹣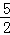 )=﹣
)=﹣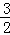 x2+4x+
x2+4x+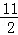 =﹣
=﹣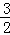 (x﹣
(x﹣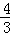 )2+
)2+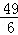 ,
,
显然﹣1<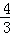 ≤
≤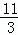 ,∴当x=
,∴当x=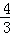 时,MN有最大值
时,MN有最大值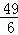 ;
;
②当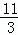 <x≤5时,MN=(
<x≤5时,MN=(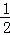 x2﹣2x﹣
x2﹣2x﹣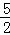 )﹣(﹣x2+2x+3)=
)﹣(﹣x2+2x+3)=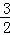 x2﹣4x﹣
x2﹣4x﹣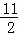 =
=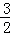 (x﹣
(x﹣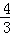 )2﹣
)2﹣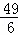 ,
,
显然当x>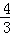 时,MN随x的增大而增大,
时,MN随x的增大而增大,
∴当x=5时,MN有最大值,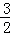 ×(5﹣
×(5﹣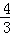 )2﹣
)2﹣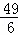 =12;
=12;
综上可知在点M自点A运动至点E的过程中,线段MN长度的最大值为12.

 名校课堂系列答案
名校课堂系列答案
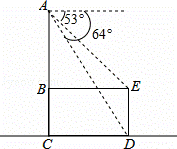
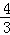 ,sin53°≈
,sin53°≈ ,tan64°≈2,sin64°≈
,tan64°≈2,sin64°≈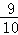 )
)
 )﹣1的值为
)﹣1的值为 

 ,
, ,且
,且 与
与 夹角为
夹角为 ,则
,则 等于
等于 B.
B. C.
C. D.
D.