题目内容
3.公式法:x2+17=8x.分析 根据求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$来解方程.
解答 解:由原方程,得
x2-8x-17=0,
∵a=1,b=-8,c=-17,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{8±\sqrt{64-4×1×(-17)}}{2}$=4±$\sqrt{33}$.
点评 本题考查了解一元二次方程--公式法.利用公式法解题时,需要弄清楚公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$中字母a、b、c所表示的含义.

练习册系列答案
相关题目
18.已知a方程2x2+3x-4=0的一个根,则代数式2a2+3a的值等于( )
| A. | 4 | B. | 0 | C. | 1 | D. | 2 |
12.下列判断错误的是( )
| A. | $\frac{2}{3}$是$\frac{4}{9}$的一个平方根 | B. | $\sqrt{2}$是$\sqrt{4}$的算术平方根 | ||
| C. | 平方根等于本身的数有0和1 | D. | (-4)2的算术平方根是4 |
13.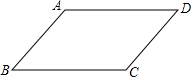 如图,下面推理中,正确的是( )
如图,下面推理中,正确的是( )
 如图,下面推理中,正确的是( )
如图,下面推理中,正确的是( )| A. | ∵∠A+∠D=180°∴AD∥BC | B. | ∵∠C+∠D=180°∴AB∥CD | ||
| C. | ∵∠A+∠D=180°∴AB∥CD | D. | ∵∠B+∠C=180°∴AD∥BC |
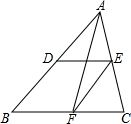 如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.
如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.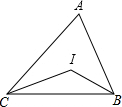 如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算:
如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算: