Question

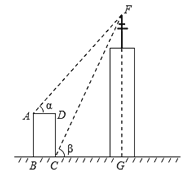
【题目】如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为∠α=48°和∠β=65°，矩形建筑物宽度AD=20m，高度CD=30m，则信号发射塔顶端到地面的高度FG为__米（结果精确到1m）．

参考数据：sin48°=0.7，cos48°=0.7，tan48°=1.1，cos65°=0.4，tan65°=2.1

Answer 1

【答案】109

【解析】

延长AD交FG于H，则四边形ABGH是矩形，AB=CD=GH=30m，AH=BG．设FH=xm．利用锐角三角函数，分别用x表示FG和CG,构建方程即可解决问题．

解：延长AD交FG于H，则四边形ABGH是矩形，AB=CD=GH=30m，AH=BG．设FH=xm

则FG=x+30．

在RtAFH中，∠α=48°，AH=，
∵AD=20m，

∴CG=DH=
在Rt△FCG中，∠β=65°，tan65°=，
∴2.1=，
∴x=79.2，
∴FG=FH+GH=109.2≈109（m），
故答案为109．