题目内容
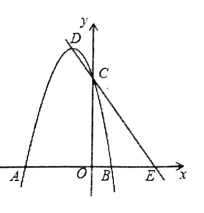
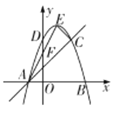
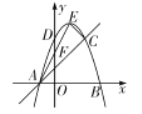
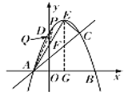
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与x轴交于A,B两点,与y轴交于点D,过点A的直线交抛物线于另一点C,点E为抛物线的顶点,连接CE,AE,设AE交y轴于点F,点A的坐标为
与x轴交于A,B两点,与y轴交于点D,过点A的直线交抛物线于另一点C,点E为抛物线的顶点,连接CE,AE,设AE交y轴于点F,点A的坐标为![]() ,且
,且![]() ,C、D两点关于对称轴对称.
,C、D两点关于对称轴对称.
(1)若![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)在(1)的条件下,试探究抛物线上是否存在一点M,使![]() 为以AC为直角边的直角三角形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由;
为以AC为直角边的直角三角形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由;
(3)设点P是直线AE上方抛物线上的一动点,若![]() 的面积最大值为
的面积最大值为![]() ,求a的值.
,求a的值.
【答案】(1)![]() ;(2)存在,点M的坐标为
;(2)存在,点M的坐标为![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)过点E作![]() 轴于点G,根据三角形中位线的性质求得点E的坐标,利用顶点式即可求得抛物线的解析式;
轴于点G,根据三角形中位线的性质求得点E的坐标,利用顶点式即可求得抛物线的解析式;
(2)作解图的辅助线,根据等腰直角三角形的判定和性质求得点![]() 的坐标,求得直线AC的解析式及与直线AC相互垂直的直线
的坐标,求得直线AC的解析式及与直线AC相互垂直的直线![]() 的解析式,联立直线
的解析式,联立直线![]() 与抛物线的解析式即可求得点
与抛物线的解析式即可求得点![]() 的坐标;
的坐标;
(3)先求得点A、B的坐标,设抛物线的表达式为![]() ,分别求得点E、F的坐标,设
,分别求得点E、F的坐标,设![]() ,求得经过A、P两点的直线解析式,利用三角形的面积公式及二次的最值即可求得答案.
,求得经过A、P两点的直线解析式,利用三角形的面积公式及二次的最值即可求得答案.
(1)如图,过点E作![]() 轴于点G,
轴于点G,
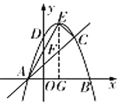
∵![]() ,
,
∴F为AE的中点,
又∵![]() ,
,
∴O为AC的中点,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点E的坐标为![]() ,
,
∵点E为抛物线的顶点,
∴设抛物线的解析式为![]() ,
,
将点![]() 代入得
代入得![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)存在.
如图,分别过点A、C作![]() ,
,![]() 分别交抛物线于点
分别交抛物线于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴于点K,过点C作
轴于点K,过点C作![]() 轴于点J,连接CD、
轴于点J,连接CD、![]() ,过点
,过点![]() 作
作![]() 于点L.
于点L.
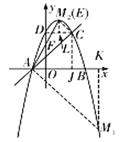
由(1)得![]() ,
,
∴![]() ,
,
∵顶点![]() ,
,
∴抛物线的对称轴为直线![]() ,
,
∵C、D两点关对称轴对称,
∴![]() ,
,
①![]() 时,
时,
∵![]() ,
,
∴∠CAJ=∠ACJ=45![]() ,
,
∴∠![]() AK=90
AK=90![]() ∠CAJ=45
∠CAJ=45![]() ,
,
∴![]() ,
,
设![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,化简得
,化简得![]() ,
,
解得 :![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
②当![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设直线AC的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,
,
将![]() ,
,![]() ,代入
,代入![]() 得:
得:
![]() ,解得
,解得![]()
∴直线AC的解析式为![]() ,
,
∵![]() ,
,
∴![]() ,即直线
,即直线![]() 的解析式
的解析式![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
联立直线![]() 与抛物线的解析式得
与抛物线的解析式得![]() ,
,
解得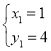 或
或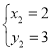 (与点C重合),
(与点C重合),
∴![]() ,即点
,即点![]() 与点E重合,
与点E重合,
综上所述,点M的坐标为![]() 或
或![]() ;
;
(3)由(1)得![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∵![]() ,
,
∴![]()
设抛物线的表达式为![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
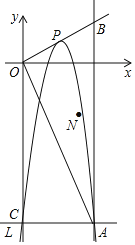
∴点P是直线AE上方抛物线上的动点,
如图,设![]() ,连接AP,直线AP与y轴交于点Q,
,连接AP,直线AP与y轴交于点Q,
设经过A、P两点的直线解析式为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴经过A、P两点的直线解析式为![]() ,
,
∴点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 的面积最大值为
的面积最大值为![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛. 并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级:A:优秀,B:良好,C:一般,D:较差),并制作了如下统计图表(部分信息未给出):
等级 | 人数 |
A | m |
B | 20 |
C | n |
D | 10 |

请根据统计图表中的信息解答下列问题:
(1)这次共抽取了________名参加演讲比赛的学生,统计图中a=________,b=________;
(2)若该校学生共有2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的有多少人?
(3)若演讲比赛成绩为A等级的学生中恰好有2名女生,其余的学生为男生,从A等级的学生中抽取两名同学参加全市演讲比赛,求抽中一名男生和一名女生的概率.