题目内容
8. 如图弓形中,AB=30$\sqrt{3}$,弓高h为15,求:
如图弓形中,AB=30$\sqrt{3}$,弓高h为15,求:(1)$\widehat{AB}$的半径R;
(2)$\widehat{AB}$的长度;
(3)弓形的面积.
分析 (1)过点O作OC⊥AB,垂足为C,交⊙O于点D,根据垂径定理得出AC=BC=$\frac{1}{2}$AB,由勾股定理得出R即可;
(2)根据三角函数先求得∠BOC=60°,继而可得$\widehat{AB}$所对圆心角度数,最后利用弧长公式求解可得;
(3)利用S弓形=S扇形AOB-S△AOB求解可得.
解答 解:(1)过点O作OC⊥AB,垂足为C,交⊙O于点D,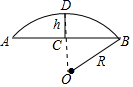
∴AC=BC=$\frac{1}{2}$AB,
∵AB=30$\sqrt{3}$,CD=h=15,
∴BC=15$\sqrt{3}$,OC=R-15,
在Rt△OBC中,OC2+BC2=OB2,
∴(R-15)2+(15$\sqrt{3}$)2=R2,
∴R=30;
(2)在Rt△OBC中,∵sin∠BOC=$\frac{BC}{BO}=\frac{15\sqrt{3}}{30}=\frac{\sqrt{3}}{2}$,
∴∠BOC=60°,
则$\widehat{AB}$所对圆心角度数为120°,
∴$\widehat{AB}$的长为$\frac{120•π•30}{180}$=20π;
(3)S弓形=S扇形AOB-S△AOB
=$\frac{120•π•3{0}^{2}}{360}$-$\frac{1}{2}$×30$\sqrt{3}$×(30-15)
=450π-225$\sqrt{3}$
点评 本题主要考查垂径定理和弧长公式、扇形的面积计算,熟练掌握垂径定理求得圆的半径是解题的关键.

练习册系列答案
相关题目
18.若a<0,ab<0,则|b-a|+1-|a-b|-3的值等于( )
| A. | 2 | B. | -2 | C. | -2a+2b+4 | D. | 2a-2b-4 |
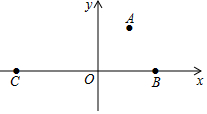
19. 如图,手掌盖住的点的坐标可能是( )
如图,手掌盖住的点的坐标可能是( )
 如图,手掌盖住的点的坐标可能是( )
如图,手掌盖住的点的坐标可能是( )| A. | (3,4) | B. | (-4,3) | C. | (-4,-3) | D. | (3,-4) |
1.一辆客车和一辆卡车同时从A地出发沿同一公路同向行驶,客车的行驶速度是70km/h,卡车的行驶速度是60km/h,客车比卡车早1h到达B地.若设A、B两地间的路程是xkm,可列方程( )
| A. | $\frac{x}{70}$-$\frac{x}{60}$=1 | B. | $\frac{x}{60}$-$\frac{x}{70}$=1 | C. | 70x-60x=1 | D. | $\frac{70}{x}$-$\frac{60}{x}$=1 |
 已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点.
已知抛物线y=ax2+bx+2经过A(1,$\frac{5}{4}$),B(2,0)和C三个点. 如图DF⊥AC于点F,BE⊥AC于点E,AB=CD,AF=CE.求证:BE=DF.
如图DF⊥AC于点F,BE⊥AC于点E,AB=CD,AF=CE.求证:BE=DF. 如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上.
如图,已知△AEB,△ACD都是等腰直角三角形,∠CAD=∠EAB=90°,求证:点A在∠EFD的角平分线上.