题目内容
16.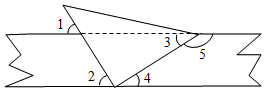 将一直角三角板与两边平行的纸条按如图所示放置,下列结论:
将一直角三角板与两边平行的纸条按如图所示放置,下列结论:①∠2=∠3; ②∠1+∠3=90°; ③∠2+∠4=180°; ④∠4+∠5=180°.其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据两直线平行同位角相等,内错角相等,同旁内角互补,及直角三角板的特殊性解答.
解答  解:∵纸条的两边平行,
解:∵纸条的两边平行,
∴∠6=∠2>45°,而∠3<45°,
∴∠2>∠3,故①错误;
∵∠1=∠6,∠6+∠3=90°,
∴∠1+∠3=90°,故②正确;
又∵直角三角板与纸条下线相交的角为90°,
∴∠2+∠4=90°,故③正确;
∵纸条的两边平行,
∴∠4+∠5=180°,故④正确;
故选:C.
点评 本题考查平行线的性质,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
7. 如图,已知a∥b,AB⊥BC于B,若∠1=55°,则∠2的度数为( )
如图,已知a∥b,AB⊥BC于B,若∠1=55°,则∠2的度数为( )
 如图,已知a∥b,AB⊥BC于B,若∠1=55°,则∠2的度数为( )
如图,已知a∥b,AB⊥BC于B,若∠1=55°,则∠2的度数为( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
4.计算:(-5)+3的结果是( )
| A. | -8 | B. | -2 | C. | 2 | D. | 8 |
11.$-\sqrt{3}+1$的倒数是( )
| A. | $-\frac{{\sqrt{3}-1}}{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | $-\frac{{1+\sqrt{3}}}{2}$ | D. | $-\frac{{1-\sqrt{3}}}{2}$ |
5.下列式子中,一定是二次根式的是( )
| A. | -$\sqrt{7}$ | B. | $\root{3}{7}$ | C. | $\sqrt{x}$ | D. | x |
6.把函数y=2x2的图象先沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度得到新函数的图象,则新函数的关系式是( )
| A. | y=2(x+3)2-2 | B. | y=2(x-3)2-2 | C. | y=2(x+3)2+2 | D. | y=2(x-3)2+2 |