题目内容
3．从一块正方形的木板上锯掉2m宽的长方形木条，剩下的面积是48m2，则原来这块木板的面积是（ ）| A． | 64m2 | B． | 100m2 | C． | 121m2 | D． | 144m2 |
分析 从一块正方形木板上锯掉2m宽的长方形木条，剩下的仍然是一个长方形，此时这个长方形的长等于原来正方形木板的边长，宽等于正方形木板的边长减去2m，根据剩下的长方形的面积是48m2，列出方程，求出解，进而求出原来正方形木板的面积．
解答 解：设原来正方形木板的边长为xm．
由题意，可知x（x-2）=48，
解得x1=8，x2=-6（不合题意，舍去）．
所以8×8=64．
故选：A．
点评 本题考查了一元二次方程的应用，理解从一块正方形木板上锯掉2m宽的长方形木条，剩下的仍然是一个长方形，是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
13．如果关于x的不等式$\left\{\begin{array}{l}2x-m≥0\\ n-3x≥0\end{array}\right.$仅有四个整数解：-1，0，1，2，那么适合这个为等式组的整数m、n组成的有序实数对（m，n）最多共有（ ）
| A． | 2个 | B． | 4个 | C． | 6个 | D． | 9个 |
11．若A是一个三位数，B是一个两位数，将A放在B的左边，那么形成的五位数为（ ）
| A． | 1000B+A | B． | 1000A+B | C． | 100B+A | D． | 100A+B |
15．在△ABC中，∠A=40°，∠B=80°，则△ABC的外心在（ ）
| A． | △ABC的内部 | B． | △ABC的外部 | C． | △ABC的边上 | D． | 不确定 |
12．在Rt△ABC中，∠C=90°，∠B=35°，AB=7，则BC的长为（ ）
| A． | 7sin35° | B． | $\frac{7}{cos35°}$ | C． | 7cos35° | D． | 7tan35° |
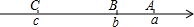如图，已知A，B，C三点分别对应数轴上的实数a，b，c，化简：|a-b|+|c-b|+|c-a|．