题目内容
 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC长是( )
如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC长是( )| A、6 | B、5 | C、4 | D、3 |
考点:角平分线的性质
专题:
分析:过点D作DF⊥AC于F,然后利用△ABC的面积公式列式计算即可得解.
解答: 解:过点D作DF⊥AC于F,
解:过点D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,
∴S△ABC=
×4×2+
AC×2=7,
解得AC=3.
故选D.
 解:过点D作DF⊥AC于F,
解:过点D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
解得AC=3.
故选D.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.

练习册系列答案
相关题目
直线y=kx+b与y=2x平行,和y轴交于点(0,3),则该函数关系式是( )
| A、y=2x-3 |
| B、y=3x+2 |
| C、y=2x+3 |
| D、y=3x-2 |
 如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、不能确定 |
在给出的四个方程中,解相同的为( )
①x-2=3;②(x-2)(x-5)=0;③2x-3=7;④x=5.
①x-2=3;②(x-2)(x-5)=0;③2x-3=7;④x=5.
| A、①② | B、①③④ | C、②③ | D、②④ |
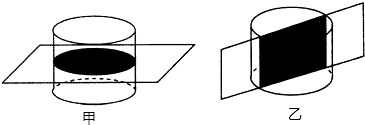 一个平面去截一个圆柱,图甲中截面的形状是
一个平面去截一个圆柱,图甲中截面的形状是 如图,直线AB与x轴、y轴分别相交于A、B点,将直线AB绕点O顺时针旋转90°得到直线A1B1,A、B点的对应点分别是A1、B1.
如图,直线AB与x轴、y轴分别相交于A、B点,将直线AB绕点O顺时针旋转90°得到直线A1B1,A、B点的对应点分别是A1、B1. 在正方形ABCD中,E是AD的中点,求tan∠ABE的值.
在正方形ABCD中,E是AD的中点,求tan∠ABE的值.