题目内容
【题目】已知抛物线
经过原点，P是抛物线的顶点．
（1）若m＝－1，k＝3时，求抛物线表达式．
（2）若抛物线
也经过P点，求a与e之间的关系式．
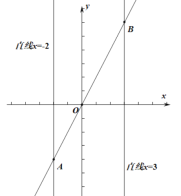
（3）若正比例函数y＝2x的图像分别交直线x＝－2，直线x＝3于A、B两点，当P在线段AB上移动时，求a的取值范围．
【答案】（1）
；（2）
；（3）
或
【解析】
（1）先将m＝－1，k＝3代入得
，再根据抛物线经过原点可求得
，进而可得抛物线的表达式；
（2）先根据抛物线
经过原点可得
，再根据
过顶点P（m，k）可得
，①+②得
，由此可得；
（3）先将（m，k）代入y＝2x中，得k＝2m，再结合
可得
，最后根据
且
即可求得答案．
解：（1）∵m＝－1，k＝3，
∴，
将（0，0）代入，得
，
解得，
∴抛物线的表达式为；
（2）∵原点，
∴，
∵过顶点P（m，k），
∴，
①+②得，，
，
，
（3）将（m，k）代入y＝2x中，得k＝2m，
，
，
，
，
且，
．
练习册系列答案
相关题目
【题目】已知甲、乙两辆汽车分别从
、
两地同时匀速出发，甲车开往地，乙车开往地，设甲、乙两车距地的路程分别为
、
（单位：
），甲车的行驶时间为
（单位：
）．若甲车的速度为
，与之间的对应关系如下表：
| 2 | 5 |
| 560 | 320 |
（1）分别求出、与之间的函数关系式；（不写的取值范围）
（2）当为何值时，甲、乙两辆汽车相遇？
（3）当两车距离小于
时，求的取值范围．
